Inhaltsverzeichnis
3 Grundschaltungen von Operationsverstärkern I
- Eine schöne Einführung bieten die Operationsverstärker-Grundschaltungen auf Microcontroller.net
- Lehr- und Arbeitsbuch Operationsverstärker (Joachim Federau) (über das Hochschulnetz einsehbar)
- Auf Youtube sind folgende zwei Videos von Prof. Griesbauer empfehlenswert: Operationsverstärker Eigenschaften, Operationsverstärker Schaltungen
- interaktive Animation eines invertierten Verstärkers ist im iPES Kurs der ETH Zürich einsehbar (Login als Gast!)
Einführendes Beispiel
Akustische Verstärker, wie sie zum Beispiel in Mobiltelefonen, Laptops oder HiFi-Anlagen vorkommen, zeigen bei starker Verstärkung häufig eine unangenehme Eigenschaft: Das vorher unverzerrte Signal wird nicht mehr wie gewohnt weitergegeben, sondern klirrt. Es wird also so verzerrt, dass es sich nicht mehr angenehm anhört.
Dazu finden Sie in Abbildung 1 und Abbildung 2 jeweils ein akustisches Beispiel mit Bildern. Im jeweiligen Bild ist unten der Zeitverlauf der an einen Lautsprecher ausgegebenen Spannung zu sehen (x-Achse: Zeit, y-Achse: Frequenz). Das obere Bild hat drei Dimensionen: Es zeigt in der Farbintensität an, welche Frequenzen zu welcher Zeit genutzt werden. Die Frequenzen in grauen Bereichen werden nicht benötigt. Wenn eine Frequenz zu einem Zeitpunkt rot dargestellt werden, so hat diese eine relativ große Amplitude.
Es ist zu sehen, dass das verzerrte Signal sowohl im Zeitverlauf der Spannung große Amplituden aufweist, als auch eine breite Verteilung an Frequenzen (= ein breites Spektrum). Gerade die hohen Frequenzen können bei Lautsprechern den Verschleiß der Membran fördern.
Die Signalverzerrung ist auf den Aufbau des Verstärkers zurückzuführen, welcher nur eine maximal mögliche Spannung ausgeben kann und ansonsten übersteuert. Der Aufbau eines akustischen Verstärkers gleicht dem eines rückgekoppelten Operationsverstärkers, so wie er in der Simulation im Folgenden zu sehen ist.
Akustische Verstärker sind meist wie Operationsverstärker aufgebaut, welche in diesem Kapitel betrachtet werden sollen.
Ziele für die Grundschaltungen von Operationsverstärkern
Nach dieser Lektion sollten Sie:
- die Grundgleichung von Operationsverstärkern und die goldenen Regeln gelernt haben.
- wissen, wie die Grundschaltungen (invertierender und nichtinvertierender Verstärker) aufgebaut sind, wie deren Spannungsverstärkung lautet und wie sich deren Ein- und Ausgangswiderstände verhalten.
- bei einfachen Verstärkerschaltungen die Spannungsverstärkung berechnen können.
- das Konzept der virtuellen Masse verstanden haben.
3.0 Einführung
Historischer Abriss
Um die Herkunft des Operationsverstärkers zu verstehen, soll hier ein kurzer Abriss der Microprozessorhistorie dargestellt werden. Der erste Mikroprozessor wurde 1971 von INTEL als Intel 4004 kommerziell vertrieben, welcher mit einem Word nur einen 4-Bit Zahlenraum darstellen konnte und eine Taktfrequenz von 500 kHz hatte. Dieser wurde bereits nach einem halben Jahr als 8008 auf ein 8-Bit Word erweitert, sodass Rechnungen wesentlich schneller durchgeführt werden konnten. Aus dieser zweiten Generation wurde 1978 der 8086 entwickelt, welcher mit einem 16-Bit Word sehr lange die Grundlage von vielen PCs und anderen Elektronikkomponenten dargestellt hatte. 1985 wurde dieser Prozessor als 80386 auf ein 32-Bit Word erweitert. Aus dieser Zeit stammt auch die vielleicht bekannte Frage, ob Software als x86 oder x64 Code installiert werden soll. Bereits seit 1999 sind Prozessoren mit 64-Bit Word verfügbar, welche aber noch nicht alle Nischen durchdrungen haben.
Mit Blick auf diesen historischen Abriss stellt sich die Frage, wie Apollo 11 die erste Mondmission sowohl die Mondfähre steuern und wie die Bahn so genau berechnet werden konnte, dass dies kein Risiko darstellt. Die Entwicklung des Apollo Gudance Computer wurde bereits 1961 gestartet, also 10 Jahre vor dem ersten kommerziellen Mikroprozessor. Dieser Prozessor konnte mit etwa 1MHz Frequenz und 16-Bit Wordbreite bereits 1966 eine Leistung bereitstellen, welche kommerziell erst 15 Jahre später zur Verfügung war. Trotzdem konnten diese Rechner nicht in vertretbarer Zeit die Differentialgleichungssysteme lösen, welche für die Trajektorienplanung notwendig waren. Dies war nur durch die Vereinigung von dem bekannten digitalen Prozessoren und den schon seit den 1920er Jahren verwendeten Analogrechnern möglich. Analogrechner erinnern nur wenig an das klassische Bild des Rechners. Sie bestehen zwar auch aus einem Netzwerk an Komponenten, besitzen aber keine Software. Vielmehr werden zur Berechnung verschiedene Eigenschaften elektronischer Komponenten genutzt (z.B. das exponentielle Verhalten der Shockley-Gleichung der Diode). Für die Apollomissionen wurde der EAI 380 Hybridrechner verwendet. Dieser und ähnliche Hybridrechner wurden noch bis in die 1990er Jahre eingesetzt um Differentialgleichungssysteme für Luft- und Raumfahrt, Baubranche und (unter etwas anderer Gestalt) auch als Synthesizer in der Musikindustrie eingesetzt. Der interessierte Leser sei auf den Vortrag von Hr. Ulmann über Analogrechner verwiesen, in welchem erklärt wird, warum diese selbst den modernsten Computern überlegen sind.
 Abb. 4: Operational Amplifier Module (OPA) in einem PIC-Microcontroller des Herstellers Microchip (c) Microchip
Abb. 4: Operational Amplifier Module (OPA) in einem PIC-Microcontroller des Herstellers Microchip (c) Microchip
Der Kernbaustein von Analogrechners ist der Operationsverstärker. Mit diesem ist es möglich Addierer, Subtrahierer, Multiplizierter, Exponenzierer, Integratoren und Differentiatoren aufzubauen und zusammenzufügen. Die „Berechnung“ geschieht, dann fast instantan nach Einstellen der gewünschten Eingangsspannungen.
Der Operationsverstärker hat diese Zeit überdauert und bietet heutzutage eine Ausgangsbasis für unterschiedlichste Signalaufbereitung, wie aktive Filter, Verstärkerstufen, Anpassung von Eingangs-/ Ausgangswiderstand und verschiedene (integrierte) Regelkreise. Bei verschiedenen Mikrocontrollern sind Operationsverstärker direkt eingebaut und können durch geeigneten Code konfiguriert werden. In Abbildung 4 ist ein PIC Microprozessor zu sehen, welcher einen integrierten Operationsverstärker enthält.
3.1 Schaltzeichen und Grundbeschaltung
Dieses Kapitel beschäftigt sich mit Operationsverstärkern bzw. im Allgemeinen mit Messverstärkern. Eine Anwendung dafür ist die Messung von Spannungen, Strömen und Widerständen. Diese müssen in einigen Anwendungen sehr genau bestimmt werden, beispielsweise für eine genaue Temperaturmessung. In diesem Fall ist eine Verstärkung der Messsignale sinnvoll und notwendig.
Diese Verstärkung geschieht durch Messverstärker. Messverstärker müssen einige Eigenschaften erfüllen:
- Messverstärker sollen keine Rückwirkung auf die Messgröße ausüben. Ein Operationsverstärker konkret soll einen möglichst großen Eingangswiderstand besitzen. Damit bricht die zu verstärkende Spannung nicht ein.
- Messverstärker sollen eine hohe Empfindlichkeit besitzen. Ein Operationsverstärker konkret soll eine große Differenzverstärkung $A_D$ aufweisen.
- Messverstärker sollen ein definiertes Übertragungsverhalten zeigen, das heißt das Ausgangssignal soll eindeutig mit dem Eingangssignal zusammenhängen. Ein Operationsverstärker konkret soll einen linearen Zusammenhang zeigen.
- Messverstärker sollen ein gutes dynamisches Verhalten zeigen. Beim Operationsverstärker konkret soll das Ausgangssignal dem Eingangssignal ohne zeitliche Verzögerung folgen.
- Messverstärker sollen ein „eingeprägtes Ausgangssignal“ erzeugen. Das bedeutet, dass die Komponenten am Verstärkerausgang das ausgegebene Signal nicht verändern können. Ein Operationsverstärker konkret soll das gewünschte Ausgangssignal mit dem dafür notwendigen Strom aufrecht erhalten können. Da der Strom $I_A$ (für elektronische Verhältnisse) sehr groß werden kann, bedeutet dies, dass ein Operationsverstärker einen geringen Ausgangswiderstand $R_A =\frac{U_A}{I_A}$ besitzen muss.
Allgemein ist ein Messverstärker wie in Abbildung 5 aufgebaut. Dies wurde bereits im Kapitel 1 Grundlagen zu Verstärkern beschrieben. Im Folgenden werden nur noch Operationsverstärker betrachtet. Ein Operationsverstärker ist ein Messverstärker, welcher häufig in der Elektrotechnik Anwendung findet.
Das Schaltsymbol des Verstärkers ist ein gleichschenkliges Dreieck, an dessen Spitze das Ausgangssignal herrührt und in dessen Basis das Eingangssignal eintritt. In Abbildung 6 sind verschiedene Schaltsymbole zu sehen:
- Schaltsymbol (1): In Blockschaltbildern (nicht zu verwechseln mit Schaltplänen, siehe Kapitel 1) wird dieses Schaltsymbol für allgemeine Verstärker verwendet. Das Eingangssignal tritt in einen Anschluss ein und über einen Anschluss aus. Dieses Zeichen wird erst wieder in Kapitel 5. zu finden sein.
- Schaltsymbol (2): Nach DIN EN 60617 ist dieses Schaltbild für Operationsverstärker zu nutzen. Es weist mit dem Unendlichzeichen auf die idealerweise unendlich hohe Verstärkung hin. im Folgenden wird dieses Symbol nicht verwendet, da dieses in allen internationalen Schaltungen und Werkzeugen nicht verwendet wird.
- Schaltsymbol (3): Das Schaltsymbol (3) ist das am häufigsten genutzte Symbol für einen Operationsverstärker. Links sind dabei der invertierende Eingang mit der Spannung $U_m$ (minus) und der nicht-invertierende Eingang mit $U_p$ (plus) zu finden. Rechts ist der Ausgang mit der Spannung $U_A$ dargestellt.
- Schaltsymbol (4): Das Schaltsymbol (4) sind zusätzlich die Versorgungsspannungen $U_{sp}$ (supply plus) und $U_{sm}$ (supply minus) mit eingezeichnet. Aus der Versorgung wird die Leistung für die ausgegebene Spannung des Operationsverstärkers bereitgestellt.
- Schaltsymbol (5) und (6): Diese Symbole zeigen keine Operationsverstärker. Diese Symbole zeigen das NOT-Gatter und das Tri-State-Gatter. Beide Komponenten sind bereits in Grundlagen der Digitaltechnik besprochen worden. Leider ist die Darstellung dieser Digitalkomponenten in verschiedenen Schaltungen dem Operationsverstärker nicht unähnlich. Ein Beispiel dazu sind die Transceiver1) SP3481 oder SP3485. Wenn digitale Eingangswerte betrachtet werden, ist davon auszugehen, dass das Schaltsymbol keinen Operationsverstärker darstellt.
Merke: Operationsverstärkereingang
Die Eingänge des Operationsverstärker sind als invertierende Eingang $U_m$ und nicht-invertierende Eingang $U_p$ bezeichnet.
Die Spannung $U_D = U_p - U_m$ wird Differenzspannung genannt
(siehe Abbildung 7).
3.2 Grundgleichung / goldene Regeln
Der Operationsverstärker ist ein Spannungsverstärker. Damit ergeben sich aus Kapitel idealisierte Verstärkergrundtypen, dass für den idealen Fall der Eingangswiderstand unendlich und der Ausgangswiderstand $R_A=0$ sein muss.
Die Abbildung 8 zeigt einen idealen Spannungsverstärker. Diese ist durch folgende Eigenschaften gekennzeichnet:
- Eingangswiderstand: In der Abbildung ist die Eingangsseite eingezeichnet. Als Widerstand wird hier der Differenzwiderstand $R_D$ angegeben, an dem die Differenzspannung $U_D$ abfällt. Es gilt also $R_D \rightarrow \infty$. Damit gehen die Eingangsströme $I_p \rightarrow 0$ und $I_m \rightarrow 0$.
- Ausgangswiderstand, Grundgleichung: Auf der Ausgangsseite ergibt sich mit $R_A=0$, dass $U_A = A_D\cdot U_D$ ist. Dies ist die Grundgleichung der Verstärkerschaltung. Im Idealfall verstärkt der Operationsverstärker linear, wie in der Gleichung angegeben. Speziell für eine Differenzspannung von $0V$ ergibt sich eine Ausgangsspannung von $0V$
- Spannungsverstärkung: Aus dem Kapitel Rückkopplung ist bekannt, dass $A_D$ sehr groß sein muss. Im Idealfall gilt: $A_D \rightarrow \infty$
Merke: Grundgleichung und goldene Regeln
- Die Ausgangsspannung hängt über die Differenzverstärkung von der Differenzspannung ab: $U_A = A_D \cdot U_D$
Dies ist die Grundgleichung der Verstärkerschaltung - Die goldenen Regeln des idealen Verstärkers lauten:
- Die Differenzverstärkung geht gegen unendlich: $A_D \rightarrow \infty$
- Der Eingangswiderstand geht gegen unendlich: $R_D \rightarrow \infty$
- Der Ausgangswiderstand ist 0: $R_A = 0$
Diese Regeln haben im realen Verstärker verschiedene Grenzen:
- $\boldsymbol{U_A = A_D \cdot U_D}$:
- Die Ausgangsspannung kann nur soweit der Eingangsspannung folgen, wie es die Spannungsversorgung zulässt. Bei realen Operationsverstärkern können nur sogenannte Rail-to-Rail Operationsverstärker den Bereich bis auf wenige $100mV$ zu $U_S$ ausnutzen. Andere Operationsverstärker haben eine Aussteuergrenze, welche vom Betrag $1...2V$ unterhalb der Versorgungsspannung liegt.
- Sind die Versorgungsspannungen nicht symmetrisch ($U_{sm} \neq -U_{sp}$), dann verschiebt sich auch die Kennlinie.
- Der ideale Operationsverstärker erzeugt die gleiche Ausgangsspannung $U_A=A_D \cdot U_D$, solange $U_D = U_p - U_m$ gleich ist. Beim realen Operationsverstärker mit festem $A_D$ unterscheidet sich Ausgangsspannung $U_{A1}$ für $U_{D1}=5V - 4,9V$ von $U_{A2}$ für $U_{D1}=0,1V - 0V$.
- $\boldsymbol{A_D}$: Die Differenzverstärkung liegt üblicherweise zwischen $A_D = 20'000 ... 400'000$.
- $\boldsymbol{R_D}$: Bei realen Operationsverstärkern ist der Eingangswiderstand $R_E > 1 M\Omega$ und der Eingangsstrom $|I_p|$ bzw. $|I_m|$ unter $1 \mu A$
- $\boldsymbol{R_A}$: Bei realen Operationsverstärkern ist der Ausgangswiderstand $R_A$ meist einige $\Omega$ groß und durch eine maximalen Strom (im Bereich von einigen Dutzend $mA$ bis wenige $A$) begrenzt
Der Operationsverstärker In der Simulation unten bildet in einigen Punkten einen realen Operationsverstärker nach: Der Die Spannungsverstärkungs beträgt $A_D = 100'000$. Die Übertragungskennlinie $U_A(U_D)$ zeigt nur dann ein proportionales Verhalten, wenn der ausgegebene Wert betragsmäßig kleiner als die (nicht abgebildete) Versorgungsspannung $|U_{sp}|=|U_{sm}|=15V$ ist. Die Aussteuergrenzen und die Spannungsverstärkung lassen sich in der Simulation über „Bauteil bearbeiten“ (Doppelklick) verändern.
Spannungsversorgung des Operationsverstärkers
Bei der Spannungsversorgung des Operationsverstärkers wird zwischen unipolar und bipolar unterschieden:
Bei der bipolaren Spannungsversorgung wird betragsmäßig die gleiche Spannung mit unterschiedlichem Vorzeichen an beide Versorgungsanschlüsse gegeben (Abbildung 9 (1)). Die Ausgangsspannung $U_A$ des Verstärkers kann dadurch in beide Richtungen zeigen (Abbildung 9 (2)). Die Spannungsversorgung muss dabei so gestaltet sein, dass sie die beiden Spannungen bereitstellen kann. Bei einer Differenzspannung von $U_D=0$ ergibt sich auch eine Ausgangsspannung von $U_A=0$.
Bei der unipolaren Spannungsversorgung liegt der negative Versorgungsanschluss auf Masse (Abbildung 9 (3)). Dadurch kann die Ausgangsspannung $U_A$ des Verstärkers nur nicht-negative Werte annehmen (Abbildung 9 (4)). Die Versorgung kann in diesem Fall durch eine einzige Spannungsquelle (z.B. eine Batterie) erfolgen. Bei einer Differenzspannung von $U_D=0$ ergibt sich eine Ausgangsspannung von $U_A=\frac{1}{2}\cdot U_{sp}$.
3.3 Spannungsfolger
Im Kapitel Rückkopplung wurde beschrieben, dass ein Verstärker mit hoher open-loop Verstärkung durch das Zurückführen eines Teils des Ausgangssignals mit negativem Vorzeichen „gebändigt“ werden kann. Im einfachsten Fall könnte das Ausgangssignal direkt auf den negativen Eingang des Operationsverstärkers gegeben werden. Am positiven Eingang wird das Eingangssignal $U_E$ der gesamten Schaltung angelegt. In Abbildung 10 ist diese Schaltung abgebildet.
Anhand dieser Schaltung soll nun das Vorgehen zum Lösen von Verstärkerschaltungen dargestellt werden.
- Ziel ist immer einen Bezug zwischen Ausgangsspannung $U_A$ und Eingangsspannung $U_E$ zu schaffen.
Daraus ergibt sich hier als Ziel die Spannungsverstärkung $A_V=\frac{U_A}{U_E}$. - Bevor gerechnet wird, sollte geprüft werden, wieviele Gleichungen das System beschreiben und damit aufgestellt werden müssen. Dies lässt sich über die Anzahl der Variablen ermitteln. Dazu werden die Ströme und Spannungen der Schaltung durchgezählt.
In diesem Fall sind es 3 Ströme und 3 Spannungen. Die Anzahl der benötigten Gleichungen ist also 6. - Nun werden Gleichungen aufgestellt, die verwendet werden können. Dazu dienen:
- Grundgleichung: (1) $U_A = U_D \cdot A_D$
- Goldene Regeln: $R_D \rightarrow \infty$ damit (2+3) $I_p = I_m = 0$, $A_D \rightarrow \infty$, $R_A = 0$
- Betrachtung der vorhandenen Maschen:
in diesem Beispiel gibt es nur eine Masche (4) $-U_E + U_D + U_A =0 $.
Achtung: Maschen können nicht durch einen Eingang in den Verstärker ein und durch den Ausgang austreten! Zu beachten ist auch die Richtung von $U_D$. - Betrachtung der vorhandenen Knoten:
in diesem Beispiel gibt es nur einen Knoten (5) $I_o = I_m$
- Es scheint eine Gleichung zu fehlen. Dies ist aber nicht richtig, denn im Ziel verbirgt sich noch eine Gleichung: (0) $A_V=\frac{U_A}{U_E}$
- Zum Lösen der Gleichungen müssen nun die Gleichungen so geschickt ineinander eingesetzt werden, dass am Ende keine Abhängigkeiten von den Variablen mehr vorhanden ist.
Die Rechnung ist hier einmal detailliert durchgeführt (der Klick auf Pfeil nach rechts „►“ führt zum nächsten Schritt, alternative Darstellung):
Die Spannungsverstärkung ist also $A_V=1$. Dies wäre auch aus Kapitel Rückkopplung zu sehen gewesen. Dort wurde hergeleitet, dass sich für $A_D\rightarrow\infty$ die Spannungsverstärkung gerade aus $k$ ergibt: $A_V=\frac{1}{k}$. Da hier die gesamte Ausgangsspannung zurückgekoppelt wird, ist $k=1$ und damit auch $A_V=1$.
Die Ausgangsspannung $U_A$ gleicht also der Eingangsspannung $U_E$. Daher rührt auch der Name „Spannungsfolger“. Man könnte nun annehmen, dass dieser Verstärker wenig hilft, denn auch eine direkte Verbindung würde $U_A=U_E$ liefern. Wichtig hier ist aber: Durch den Operationsverstärker gibt es keine Rückwirkung von U_A auf U_E. Dies bedeutet, dass ein Widerstand auf der Ausgangsseite die Eingangsseite nicht belastet. In der Simulation rechts kann durch den Slider „Resistance“ (rechts) der Lastwiderstand geändert werden. Dadurch ändert sich zwar der Stromfluss, aber nicht die Spannung.
Dieses Verhalten lässt sich auch anders erklären: Das Eingangssignal kommen meist aus einer Spannungsquelle, welche nur geringe Ströme erzeugen kann. Das heißt die Eingangssignale sind hochohmig ($\text{hochohmig}=\frac{\text{Spannung}}{\text{kleinen Strom}}$). Am Ausgang kann aber eine Last beliebiger Impedanz anliegen. Das heißt, um das Ausgangssignal konstant zu halten, muss je nach Last ein großer Strom bereitgestellt werden. Da der Ausgangswiderstand das Verstärkers gegen 0 geht, ist das Signal tatsächlich niederohmig ($\text{niederohmig}=\frac{\text{Spannung}}{\text{u.U. großen Strom}}$). Daher rührt auch der zweite Name der Schaltung „Impedanzwandler“.
Merke: Schritte zum Ziel
Zum Lösen von Aufgaben hilft folgendes Vorgehen:
- Wohin? Klärung des Ziels (hier: stets die Beziehung zwischen Ausgangs- und Eingangssignal)
- Woran? Klärung was dazu benötigt wird (hier: stets Gleichungen. Anzahl der Gleichungen durch Variablenanzahl ermittelbar)
- Womit? Klärung was bereits vorhanden ist (hier: bekannte Gleichungen: Spannungsverstärkungsgleichung, Grundgleichung, goldene Regeln, Maschen-/Knotensatz, Beziehungen von Spannungen und Strömen der Komponenten)
- Go! Lösung erarbeiten (hier:Einsetzen der Gleichungen)
Es hilft dabei die Gleichung so umzustellen, dass $1/A_D$ ohne Vorfaktor erscheint. Es gilt: $1/A_D \xrightarrow{A_D \rightarrow \infty} 0$
3.4 Nichtinvertierender Verstärker
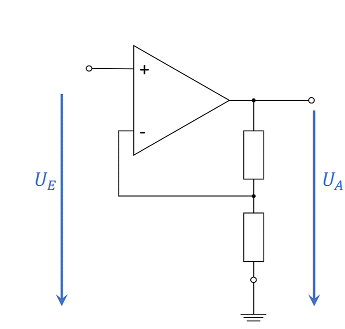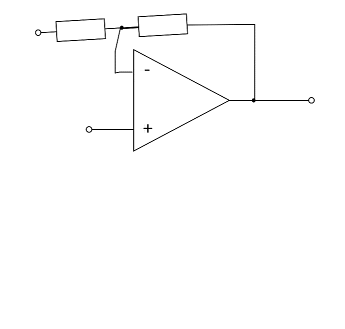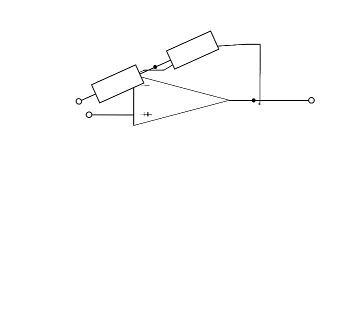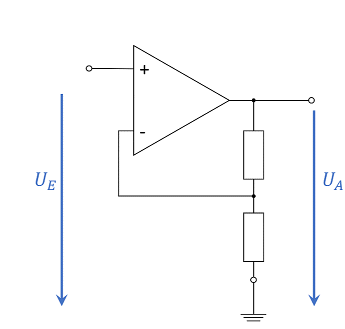
Bisher wurde die gesamte Ausgangsspannung gegengekoppelt. Nun soll nur ein Teil der Spannung zurückgeführt werden. Dazu kann die Ausgangsspannung über einen Spannungsteiler $R_1+R_2$ verringert werden. Die Schaltung dazu ist in Abbildung 11 zu sehen.
Über die Betrachtung der Rückkopplung kann auch hier das Ergebnis schnell hergeleitet werden: von der Ausgangsspannung $U_A$ wird nur $\frac{R_2}{R_1+R_2}\cdot U_A$ zurückgeleitet. Der Rückkoppelfaktor ist also $k=\frac{R_2}{R_1+R_2}$ und damit wird die Spannungsverstärkung $A_V=\frac{R_1+R_2}{R_2}$.
Dieser „Trick“ über $A_V=\frac{1}{k}$ ist bei einigen der folgenden Schaltungen nicht mehr möglich. Entsprechend soll auch hier eine mögliche Lösung über die Netzwerkanalyse hergeleitet werden.
Aufgabe 3.4.1 nichtinvertierender Verstärker
Leiten Sie für den nichtinvertierenden Verstärker die Spannungsverstärkung her. Nutzen Sie dabei das Vorgehen, welches für den Spannungsfolger verwendet wurde.
| Schritt | Beschreibung | Umsetzung |
|---|---|---|
| 1 | Was ist gesucht? | $A_V = \frac{U_A}{U_E}=?$ |
| 2 | Zählen der Variablen $\rightarrow$ Anzahl der notwendigen Gleichungen | 5 Spannungen + 5 Ströme $\rightarrow$ Anzahl der notwendigen Gleichungen: 10 |
| 3 | Aufstellen der Gleichungen | (1) Grundgleichung: $U_A = A_D \cdot U_D$
Goldene Regeln: $R_D \rightarrow \infty$, damit (2+3) $I_p \rightarrow 0$ und $I_m \rightarrow 0$ $R_A = 0$ $A_D \rightarrow \infty$ (siehe ) (4) Masche I: $-U_E + U_D + U_2 = 0$
(5) Masche II: $-U_2 -U_1 + U_A = 0$ (6) Knoten I: $I_o = I_1$ (7) Knoten II / Spannungsteiler: $I_1 - I_2 - I_m = 0$
(8) Widerstand $R_1= \frac{U_1}{I_1}$ (9) Widerstand $R_2= \frac{U_2}{I_2}$ |
Die Rechnung ist hier noch einmal detailliert durchgeführt (der Klick auf Pfeil nach rechts „►“ führt zum nächsten Schritt, alternative Darstellung):
Die Spannungsverstärkung des nicht invertierenden Verstärkers ist also $A_V=\frac{R_1+R_2}{R_2}$ bzw. $A_V=1+\frac{R_1}{R_2}$. Der Zahlenwert $A_V$ kann also nur größer als 1 werden. In der Simulation rechts ist dies nochmals dargestellt. In realen Schaltungen werden die Widerstände $R_1$ und $R_2$ im Bereich zwischen einigen $100 \Omega$ und wenigen $M\Omega$ liegen. Ist die Summe der Widerstände zu klein, wird der Operationsverstärker stark belastet. Der Ausgangsstrom darf aber den Maximalstrom nicht überschreiten. Ist die Summe der Widerstände zu groß, kann der Strom $I_1=I_2$ in den Bereich des Strom $I_m$ kommen, welcher im realen Operationsverstärker vorhanden ist.
Es soll hier auch der Eingangs- und Ausgangswiderstand der gesamten Schaltung betrachtet werden. Beide Widerstände werden hier mit einer hochgestellten 0 gekennzeichnet, um diese vom Eingangs- und Ausgangswiderstand des Operationsverstärkers zu unterscheiden. Der Eingangswiderstand $R_{E}^0$ ist gegeben durch $R_{E}^0=\frac{U_E}{I_E}$ mit $I_E=I_p$. Für den idealen Operationsverstärker gilt also auch, dass der Eingangswiderstand $R_{E}^0=\frac{U_E}{I_p} \rightarrow \infty$ wird, wenn $I_p \rightarrow 0$.
Im realen Fall ist wichtig, in wiefern der gesamte Eingangswiderstand vom Eingangswiderstand des Operationsverstärkers abhängt $R_{E}^0(R_D)$. Dies lässt sich folgendermaßen ableiten: (der Klick auf Pfeil nach rechts „►“ führt zum nächsten Schritt, alternative Darstellung):
Es lässt sich also vereinfachend mitnehmen, dass der Eingangswiderstand der gesamtem Schaltung um ein Vielfaches höher ist, als der des Operationsverstärkers. Der Ausgangswiderstand $R_A^0$ der gesamten Schaltung mit realen Operationsverstärkern soll nur skizziert werden: In diesem Fall ist der Ausgangswiderstand $R_A$ des Operationsverstärkers parallel zu $R_1 + R_2$. Damit wird der Ausgangswiderstand $R_A^0$ etwas kleiner sein, als $R_A$.
Merke: nichtinvertierender Verstärker
Beim nichtinvertierenden Verstärker gilt:
- Die Eingangsspannung $U_E$ liegt am nichtinvertierenden Eingang des Operationsverstärkers
- Die Rückkopplung geschieht über einen Spannungsteiler $R_1 + R_2$
- Die Spannungsverstärkung beträgt $A_V=\frac{R_1+R_2}{R_2}$ bzw. $A_V=1+\frac{R_1}{R_2}$ und ist immer größer als 1
- Sowohl Eingangs- als auch Ausgangswiderstand der Gesamtschaltung sind kleiner als diese beim verwendeten (realen) Operationsverstärker
3.5 Invertierender Verstärker
Die Schaltung des invertierenden Verstärkers lässt sich aus der des nichtinvertierenden Verstärkers ableiten (siehe Abbildung 13). Hierzu betrachtet man zunächst den nichtinvertierenden Verstärker als ein System mit 3 Anschlüssen (bzw. als Vierpol): $U_E$, $GND$ und $U_A$. Diese Anschlüsse können - unter Beibehaltung des Ausgangsanschlusses $U_A$ - umsortiert werden. Damit liegt der Spannungsteiler $R_1 + R_2$ nun nicht mehr zwischen $U_A$ und $GND$, sondern zwischen $U_A$ und $U_E$, siehe Abbildung 12.
Bei dieser Schaltung wird der Widerstand $R_2$ auch als Gegenkopplungswiderstand bezeichnet.
Bevor die Spannungsverstärkung ermittelt wird, soll zunächst der Knoten $K1$ in Abbildung 12 betrachtet werden. Dieser ist gerade um die Spannung $U_D$ größer als das Massepotential; er liegt also auf der Potentialdifferenz $U_D$. Bei einem rückgekoppelten Verstärker mit endlicher Spannungsversorgung kann $U_A$ nur endlich sein und damit geht $U_D= U_A / A_D \rightarrow 0$ (vgl. Grundgleichung des Operationsverstärkers), da $A_D \rightarrow \infty$ gilt. Damit ist ersichtlich, dass der Knoten $K1$ beim idealen Operationsverstärker immer auf Massepotential liegt. Diese Eigenschaft nennt man virtuelle Masse, da kein direkter Kurzschluss zu Masse besteht. Vielmehr regelt der Operationsverstärker seine Ausgangsspannung $U_A$ gerade so, dass das der Spannungsteiler dadurch gerade am Knoten $K1$ ein Potential von $0V$ einstellt. Dies ist auch in der Simulation durch den Spannungsverlauf an $K1$ zu sehen.
Merke: Virtuelle Masse
Beim idealen, rückgekoppelten Verstärker gilt: $U_D \rightarrow 0$. Damit liegt an beiden Eingängen immer die gleiche Spannung an. ist eine der beiden Spannungen fest vorgegeben, z.B. durch Anschluss von Massepotential oder auch durch eine feste Spannungsquelle, nennt man diese Eigenschaft virtuelle Masse.
Für die Ermittlung der Spannungsverstärkung scheint hier die Betrachtung der Rückkopplung $A_V=\frac{1}{k}$ zunächst wenig zu bringen. Stattdessen ist aber die Ermittlung über Netzwerkanalyse möglich. Abbildung 12 zeigt dazu eine mögliche Variante die Maschen zu wählen. Die Netzwerkanalyse soll hier jedoch nicht erfolgen, sondern ist als Aufgabe 3.5.1 unten angegeben.
Stattdessen soll hier zwei andere Arten der Herleitung gezeigt werden, um weitere Herangehensweisen näher zu bringen. Für die erste Herleitung wird der Spannungsteiler $\boldsymbol{R_1 + R_2}$ betrachtet. Beim unbelasteten Spannungsteiler gilt allgemein:
\begin{align*} U_2 = U_{12} \cdot \frac{R_2}{R_1 + R_2} \end{align*}
Diese Gleichung soll nun für die konkrete Verwendung angepasst werden. Zunächst Abbildung 12 lassen sich die Spannungen des Spannungsteilers wie in Abbildung 14 angegeben, ablesen. Daraus ergibt sich mit der allgemeinen Spannungsteiler-Formel:
\begin{align*} U_2 = ( U_E - U_A ) \cdot \frac{R_2}{R_1 + R_2} \end{align*}
Mit der virtuelle Massen am Knoten $K1$ in Abbildung 14 gilt, dass $U_2$ von der (virtuellen) Masse wegzeigt und damit betragsmäßig $U_A$ gleicht. Durch die gleiche Argumentation gilt $U_E = U_1$. Es ergibt sich also:
\begin{align*} - U_A = ( U_E - U_A ) \cdot \frac{R_2}{R_1 + R_2} \end{align*}
Und daraus:
\begin{align*} - U_A &= U_E \cdot \frac{R_2}{R_1 + R_2} - U_A \cdot \frac{R_2}{R_1 + R_2} \\ - U_A + U_A \cdot \frac{R_2}{R_1 + R_2} &= U_E \cdot \frac{R_2}{R_1 + R_2} \\ U_A \cdot ( \frac{R_2}{R_1 + R_2} - 1) &= U_E \cdot \frac{R_2}{R_1 + R_2} \\ \frac{U_A}{U_E} &= \frac{\frac{R_2}{R_1 + R_2}}{ \frac{R_2}{R_1 + R_2}-1} \\ \frac{U_A}{U_E} &= \frac{R_2}{ R_2 - (R_1 + R_2)} = \frac{R_2}{-R_1} \\ \\ \boxed{A_V = - \frac{R_2}{R_1}} \end{align*}
Für eine zweite Herleitung soll der Stromfluss durch die Widerstände $R_1$ und $R_2$ des unbelasteten Spannungsteilers betrachtet werden. Diese beiden Ströme $I_1$ und $I_2$ sind gerade gleich. Damit gilt:
\begin{align*} I_\boxed{}=\frac{U_\boxed{}}{R_\boxed{}}=const. \quad \text{mit} \: \boxed{}=\{1,2\} \end{align*}
bzw.
\begin{align*} \frac{U_1}{R_1}=\frac{U_2}{R_2} \end{align*}
Dies lässt sich auch über ähnliche Dreiecke in eine „Wippe“ bzw. ein mechanisches Analogon umwandeln. Im mechanischen Analogon sind die Potentiale über die Höhe gegeben. Wie im elektrischen Fall mit dem Massepotential muss im mechanischen Bild eine Höhenbezugsebene gewählt werden. Die elektrischen Ströme entsprechen Kräfte (also einem Impulsfluss) - die Betrachtung der Kräfte ist hier aber nicht notwendig. 2).
Wird nun eine bestimmte Höhe (Spannung $U_E$) eingestellt, so ergibt sich über Kraftarm (Widerstand $R_1$) und Lastarm (Widerstand $R_2$) eine bestimmte Höhe auf der rechten Seite (Spannung $U_A$). Dies ist in Abbildung 15 oben dargestellt. In der Abbildung können alle rot markierten Punkte () manipuliert werden. Entsprechend ist die Eingangsspannung $U_E = U_{in}$ einstellbar und ergibt automatisch eine Spannung $U_A=U_{out}$. In der Schaltung (Abbildung unten) können die Widerstände $R_1$ und $R_2$ geändert werden.
Der Eingangswiderstand der gesamten Schaltung $R_E^0=\frac{U_E}{I_E}$ ergibt sich leicht aus der Betrachtung der Eingangsseite: Da $K1$ auf $0V$ liegt, ist $U_1 = U_E$. Der komplette in den Eingang einfließende Strom durchquert den Widerstand $R_1$. Es gilt dann also, dass er Eingangswiderstand $R_E = R_1$ ist. Beim Ausgangswiderstand der gesamten Schaltung $R_A^0$ ergibt sich wieder eine Parallelschaltung zwischen dem Ausgangswiderstand des Operationsverstärkers $R_A$ und dem Widerstand $R_2$. Der Ausgangswiderstand wird also etwas kleiner sein als der Ausgangswiderstand des Operationsverstärkers $R_A$.
Merke: Invertierender Verstärker
Beim invertierenden Verstärker gilt:
- Die Eingangsspannung $U_E$ liegt am invertierenden Eingang des Operationsverstärkers
- Die Rückkopplung geschieht über einen Spannungsteiler aus $R_1$ und $R_2$.
- Die Spannungsverstärkung beträgt $A_V= - \frac{R_2}{R_1}$ und ist immer kleiner als 0. Der Betrag der Spannungsverstärkung kann aber größer oder kleiner als 1 sein.
- Der Eingangswiderstand der Gesamtschaltung sind über $R_1$ definiert und i.d.R. kleiner als der beim verwendeten (realen) Operationsverstärker.
Der Ausgangswiderstand ist kleiner als der beim verwendeten (realen) Operationsverstärker.
Aufgaben
Aufgabe 3.3.1 Analyse der Impedanzwandler-Schaltung mit unterschiedlichen Operationsverstärkern
Stellen Sie sich vor, dass Sie in der Firma „HHN Mechatronics & Robotics“ arbeiten, welche ein günstiges mobiles EKG – also ein Messgerät für das Elektrokardiogramm, bzw. die Herzspannungskurve – für Sportler und Bedürftige aufbauen möchte. Das Messsignal hat dabei nur wenige Millivolt und Mikroampere. Um das Signal auf dem Weg von der aufgeklebten Elektrode zur Auswerteelektronik vor elektromagnetischer Einstrahlung zu schützen, ist eine Abschirmung um die Leitung gelegt (siehe Abbildung 16, oben). Da dadurch aber ein parasitärer Kondensator aufgebaut wird, hat Ihnen ein Kollege eine aktive Schirmung vorgeschlagen. Dabei wird die Abschirmung über einen Spannungsfolger immer auf der Messspannung gehalten, welche an der Leitung anliegt (siehe Abbildung 16, unten). Der parasitäre Kondensator wird durch diesen Aufbau nie geladen, da auf seinen beiden Seiten die gleiche Spannung herrscht - es entsteht keine Verfälschung des Signals. Wichtig ist für die Anwendung, dass der Spannungsfolger schnell reagiert.
Sie sind mit der Auslegung dieses Spannungsfolgers betreut und sollen die verfügbaren Operationsverstärker $LM318$, $uA741$ und $uA776$ in der Spannungsfolger-Schaltung (vgl. Skript Seite) analysieren.
Es ist ein kurzer Bericht (Problembeschreibung, Schaltung aus Tina, Ergebnisse, Diskussion) zu erstellen; als Analysewerkzeug ist Tina TI zu verwenden.
- Bilden Sie die oben beschriebene Schaltung für einen realistischen Operationsverstärker in Tina nach. Nutzen Sie dabei als Quelle einen Spannungsgenerator als Sprungfunktion („Unit step“) mit der Amplitude $U_A = 1,0 V$ .
- Simulieren Sie über „Analysis“»“Transient…“ für die angegebenen Operationsverstärker den Zeitverlauf.
Bestimmen Sie jeweils die Zeit die verstreicht bis der Ausgangswert von $0,1 V$ zum ersten mal $0,9 V$ erreicht (10% bis 90% der Amplitude, auch Anstiegszeit genannt). - Beschreiben Sie jeweils den Zeitverlauf. Gibt es neben der Anstiegszeit weitere Unterschiede?
- Welchen der drei Operationsverstärker würden Sie – auf Basis der angegebenen Informationen – für das Problem wählen?
Vertiefende Informationen (nicht relevant für Hausarbeit):
- Masterarbeit zu Entwicklung und Bau eines Demonstrationsmessgeräts
- Detaillierte Beschreibung einer EMG/EKG Vorverstärkerschaltung
Aufgabe 3.3.2 Zusatzaufgabe zu 3.3.1
Bei dieser Aufgabe soll auch von der gleichen Fragestellung wie in Aufgabe 3.3.1 ausgegangen werden. Diesmal soll aber der Einfluss des Impedanzwandlers auf das Sensorsignal analysiert werden. Der Signalverlauf der EKG-Spannung muss dazu durch die Spannungsquelle nachgebildet werden. Wählen Sie dazu als Spannungsquelle „Piecewise linear“ (3. von rechts) und verwenden Sie untenstehenden Verlauf.
Außerdem muss der Einfluss auf den Strom (=Ausganswiderstand des Sensors) berücksichtigt werden. Fügen Sie dazu jeweils direkt vor den nicht-invertieren Eingängen einen Widerstand mit 20 MOhm ein.
- Simulieren Sie nun den Zeitverlauf für 0 s bis 2 s mit „Use initial conditions“.
- Welchen einzigen Unterschied zeigen die ausgegebenen Signale? (y-Achse beachten)
- Für den realen Operationsverstärker müssen im Ersatzschaltbild 3 weitere Stromquellen und eine weitere Spannungsquelle berücksichtigt werden (vgl. Bild rechts). In Tina können die Werte dieser Stromquellen in den Spezifikationen des simulierten Operationsverstärker betrachtet werden (Doppelklick auf den OPV in Schaltung » Type … » Model Parameters). Aus die Analyse der gesamten Schaltung (incl. Ersatzschaltbild) soll hier nicht eingegangen werden. Es wird davon ausgegangen, dass der „input bias current“ der Operationsverstärker der ausschlaggebende Wert ist.
Vergleichen Sie die Werte der verschiedenen Operationsverstärker. - Überlegen Sie sich vereinfachend, welche zusätzliche Eingangsspannung sich durch den Strom einer einzelnen Bias-Stromquelle am Sensorwiderstand ergibt.
Aufgabe 3.3.3 Verwendung von Verstärkern in Microcontrollern
In den Application Notes MTP3132 des Herstellers Microchip ist auf der 2. Seite ein Blockdiagramm gegeben, welches die Verwendung des Operationsverstärker-Moduls verschiedener PIC-Controller erklärt.
- Im Blockdiagramm ist das logische Eingangssignal „UG“ eingezeichnet. Was passiert in der logischen Schaltung, wenn dieses den Wert TRUE annimmt?
- Welche Operationsverstärkerschaltung wird dadurch eingestellt?
- Zu welchem Zweck wird diese eingestellte Operationsverstärkerschaltung verwendet?
Aufgabe 3.4.2 Eingangswiderstand von rückgekoppelten Systemen
Im Kapitel 3.4.2 wurde der Ausgangswiderstand vom nichtinvertierenden Verstärker berechnet. Ermitteln Sie analog das Verhältnis zwischen dem Eingangswiderstand $R_{e,cL}$ einer closed-loop Verstärkerschaltung und dem open-loop Eingangswiderstand $R_{e,oL}$.
Aufgabe 3.5.1 invertierender Verstärker
Leiten Sie für den invertierenden Verstärker die Spannungsverstärkung her. Nutzen Sie dabei das Vorgehen, welches für den nicht-invertierenden Verstärker verwendet wurde.
Berücksichtigen Sie, dass für die Differenzverstärkung $A_D$ des idealen OPV gilt: $A_D \rightarrow \infty$.
Damit ist gilt auch: $1/A_D \rightarrow 0$ , aber es gilt nicht immer ${{C}\over{U_x \cdot A_D}} \rightarrow 0$, für eine unbekannte Kontante $C$ und eine Spannung $U_x$!
- Was ist gesucht?
- Anzahl der Variablen?
- Anzahl der notwendigen Gleichungen?
- Aufstellen der bekannten Gleichungen
- Herleitung der Spannungsverstärkung
- Welcher der Verstärker (invertierender oder nicht invertierender) hat einen geringeren Eingangswiderstand? Warum?
Aufgabe 3.5.2. Variationen des nicht-invertierenden Verstärkers
Auf den folgenden Seiten finden Sie Schaltungen mit einem idealen Operationsverstärker, welche dem nicht-invertierenden Verstärker ähneln und deren Spannungsverstärkung $A_V$ zu ermitteln ist.
Annahmen
- $R_1 = R_3 = R_4 = R$
- $R_2 = 2 \cdot R$
- $U_E$ entstammt einer niederohmigen Quelle
- $U_A$ liegt an einem hochohmigen Verbraucher an
Aufgaben
- Geben Sie für jede Schaltung die Spannungsverstärkung $A_V$ an. Eine detaillierte Rechnung wie bisher ist nicht notwendig.
- Geben Sie für die Abbildung 7 an, wie die Spannungsverstärkung ermittelt werden kann.
- Verallgemeinern Sie mit Begründung wie
- ein Kurzschluss der beiden OPV Eingänge zu berücksichtigen ist,
- Widerstände zu berücksichtigen sind, wenn diese
- mit einer Klemme („auf einer Seite“) direkt und ausschließlich an einem OPV Eingang liegen,
- mit je einer Klemme direkt an einem OPV Eingang liegen.
- In welchen Schaltungen stellen die Widerstände $R_3$ und $R_4$ einen unbelasteten Spannungsteiler dar?
Um sich den Problemen zu nähern, sollten Sie versuchen die Kenntnisse aus dem invertierenden Verstärker nutzen. Es kann sich anbieten die Schaltungen über Falstad-Circuit oder Tina TI zu simulieren. Als Unterstützung sind in den ersten beiden Schaltungen Tipps unter der Abbildung zu sehen.
Wichtig: Wie immer im Studium sollten Sie versuchen die Kenntnisse aus der Aufgabe zu verallgemeinern.
Tipps
- Wie groß ist der Stromfluss in den invertierenden und nicht invertierenden Eingang bei einem idealen Operationsverstärker? Welchen Spannungsabfall würde es also an einem Widerstand geben, dessen einer Anschluss nur zu einem Eingang des Operationsverstärkers führt?
- Der Operationsverstärker versucht stets soviel Strom am Ausgang auszugeben, damit sich zwischen invertierendem und nicht invertierendem Eingang die benötigte minimale Spannung $U_D$ ergibt. Wie groß kann $U_D$ angenommen werden? Kann diese Spannung auch über einen Widerstand aufgebaut werden?
- Können verschiedene Widerstände (z.b. weil diese zwischen den gleichen Knoten liegen) zusammengefasst werden?
Abb. 1

Abb. 2

Abb. 3

Abb. 4

Abb. 5

Abb. 6

Abb. 7

Abb. 8

Abb. 9

Aufgabe 3.5.3. R-2R-Leiter
Sie arbeiten in der Firma „HHN Mechatronics & Robotics“, welche für einen Kunden ein Batteriemodell aufbauen soll. Dieses Modell soll eine reale Batterie nachbilden. Dazu soll eine Spannung ausgegeben werden, welche durch ein Softwaremodell der Batterie vorgegeben wird. Es wird also ein Digital-Analog-Wandler (engl. Digital-Analog-Converter, DAC) benötigt.
Sie haben dafür den DAC7741 gefunden. Im Datenblatt sehen Sie auf Seite 12 ein Abbild des internen Aufbaus - diese gleicht der Abbildung rechts. Für eine Fehleranalyse wollen Sie nun diesen Aufbau näher verstehen.
In der Zeichnung rechts steht die aktuelle Schalterstellung für 000b, also alle Schalter $SW_1$ … $SW_3$ sind nach Masse geschalten. Es bietet sich an die Schaltung in Falstad-Circuit zum besseren Verständnis nachzubauen. In diesem Fall bietet es sich an die einzlenen Knotenspannungen $K_1$ … $K_3$ mit zu messen.
- Es soll nun zunächst $SW_3$ = 1, $SW_2$ = 0 und $SW_1$ = 0 gelten - also nur der Schalter $SW_3$ ist auf $U_{logic}$ geschalten.
- Zeichnen Sie dazu das Ersatzschaltbild ohne Schalter.
- Vereinfachen Sie dieses Ersatzschaltbild über einen Ersatzwiderstand.
- Es ergibt sich dabei ein Widerstand, welcher zwischen invertierendem und nicht invertierendem Eingang liegt. Der Operationsverstärker versucht stets soviel Strom das ihm umgebende Widerstandsnetz einzuspeisen, dass sich eine geringe Differenzspannung $U_D$ ergibt. Dies ist auch bei einem (nicht zu kleinen) Widerstand zwischen invertierendem und nicht invertierendem Eingang möglich.
Welche Verstärkung ergibt sich also?
- Es soll nun $SW_3$ = 0, $SW_2$ = 1 und $SW_1$ = 0 gelten - also nur der Schalter $SW_3$ ist auf $U_{logic}$ geschalten.
- Zeichnen Sie auch hier das Ersatzschaltbild ohne Schalter.
- Vereinfachen Sie auch dieses Ersatzschaltbild über Ersatzwiderstände.
- Auch hier gilt die Aussage über den oben genannten Widerstand zwischen invertierendem und nicht invertierendem Eingang. Weiterhin sollte Ihnen die Spannung des Knotens $K_3$ klar sein.
Zeichnen Sie nun ein Ersatzschaltbild der linken Seite, wobei Sie die Spannung am Knotens $K_3$ des idealen Verstärkers annehmen. - Ermitteln Sie nun die Spannung am Knoten $K_2$.
- Diese Spannung am Knoten $K_2$ ist die Eingangsspannung eines invertierende Verstärkers, welcher vom Knoten $K_2$ an nach rechts beginnt. Berechnen Sie nun die Verstärkung des sich so ergebenden Netzes.
- Inzwischen sollte das Konzept verstanden haben. Geben Sie nun an, welcher Eingang/welcher Schalter das LSB angibt.
Aufgabe 3.5.4. Umwandlung eines bipolaren Signals in ein unipolares Signal
Sie arbeiten in der Firma „HHN Mechatronics & Robotics“ und sollen in einem Projekt aus einem unipolaren Signal eines Digital-Analog-Wandler (0..5V) ein bipolares Signal (-10V..+10V) erzeugen. Ein Kollege hat Ihnen dazu rechtsstehende Schaltung empfohlen.
- Analysieren Sie zunächst, welche Änderung durch Drücken des Schalters S erfolgt. Wie ändert sich das Ausgangssignal?
- Versuchen Sie durch Superposition die Beziehung von $U_A$ und $U_E$ als $U_A(U_E)$ mathematisch zu bestimmen.
- Die Schaltung hat noch das Problem, dass die positive Halbwelle negativ ausgegeben wird. Welche weitere Schaltung muss dahinter vorgesehen werden, damit dieses Problem gelöst werden kann?
Lernfragen
- Erklären Sie den Unterschied zwischen unipolarer und bipolarer Spannungsversorgung eines OPV.
- Zeichnen Sie eine Skizze für bipolarer und eine für unipolare Spannungsversorgung.
- Welche Vor- und Nachteile haben uni- und bipolare Versorgung bei OPV?
- Was bedeutet „virtuelle Masse“? Unter welchen Umständen ist diese in Operationsverstärker-Schaltungen zu finden?
- Wie lauten die goldenen Regeln bei gegengekoppelten Verstärkerschaltungen?
- Wie lautet die Grundgleichung bei gegengekoppelten Verstärkerschaltungen?
- Wofür werden Impedanzwandler eingesetzt?
- Wie verhält sich die Eingangsspannung zu der Ausgangsspannung bei einem Impedanzwandler und warum?
- Was bedeutet „Spannungsfolger“ im Zusammenhang mit Operationsverstärkern und was sind die Eigenschaften des Spannungsfolgers?
- Referenzen zu den genutzten Medien
-
Element Lizenz Link Abbildung 4: Bild mit internem Operationsverstärker (c) Microchip http://ww1.microchip.com/downloads/en/appnotes/90003132a.pdf <--
1) „transmitter und receiver“, also Sender-Empfänger, bzw. Schnittstellenadapter2) Um das mechanische Analogon des Aufbaus zu komplettieren, kann man annehmen, dass es eine äußere „Kraftquelle“ gibt. Dieser agiert stets so, dass er dem der virtuellen Masse entsprechenden Punkt immer auf der Höhenbezugsfläche landet.