Inhaltsverzeichnis

2 Dioden und Transistoren

Eine schöne Einführung ist im KIT Brückenkurs - 1.5.3 Dioden und Transistoren (*) zu finden.
Aus dieser Einführung sind einige der folgenden Passagen, Videos und Bilder entnommen.

Eine weitere Einführung finden Sie unter LEIFIphysik.

Einführendes Beispiel

Die Elektronik in PCs, Mobiltelefonen, elektrischen Zahnbürsten und wie allen anderen digitalen Begleitern basiert auf Transitorschaltungen (vgl. im Herzen eines Computers). In Grundlagen der Digitaltechnik wurde bereits erläutert, dass alle logischen Schaltungen über konjunktive und disjunktive Normalform auf NAND bzw. NOR Gatter zurückgeführt werden kann. Diese wiederum bestehen aus Transistoren. In der unten stehenden Simulation ist die Struktur eines NAND-Gatters in der aktuellen CMOS-Struktur dargestellt. CMOS deutet hierbei auf die Struktur der Schaltung und der Halbleiter Struktur hin: Complementary metal-oxide-semiconductor - eine gegensätzlich ergänzende Schaltung aus Halbleitern der Struktur Metall-Oxid-Halbleiter. Die komplementäre Struktur zeigt sich darin, dass

  • vom digitalen Ausgang ($OUT2$) zur Masse zwei Transistoren einer Art in Reihe geschalten sind und
  • vom digitalen Ausgang ($OUT2$) zur 5V-Versorgung zwei Transistoren einer anderen Art parallel geschalten sind.

Diese zwei unterschiedliche Arten von MOS-Transistoren und weitere verwendete Arten sollen in diesem Kapitel erklärt werden.

Ziele für den Bipolartransistor

Nach dieser Lektion sollten Sie:

  1. wissen, welche Arten von Bipolartransistoren es gibt, wie deren Schichtstruktur und das Schaltsymbol aussieht.
  2. wissen, wie die beiden Arten von Bipolartransistoren angesteuert werden.
  3. wissen, welche die wichtigsten Kennfelder des Bipolartransistors sind und wie diese aussehen.

Ziele für den Feldeffekt-Transistor

Nach dieser Lektion sollten Sie:

  1. wissen, welche Arten von MOSFETs es gibt, wie deren Schichtstruktur und das Schaltsymbol aussieht.
  2. wissen, welche das Ausgangskennlinienfeld des MOSFETs aussieht.
  3. wissen, was die Bodydiode ist und woher diese herrührt.
  4. wissen, was bei der Auslegung eines Halbleiterelements im Ausgangskennlinienfeld zu beachten ist.

2.6 Funktionsprinzip eines (Bipolar-)Transistors

Aus der Diode bzw. dem PN-Übergang heraus lässt sich ein veränderbarer Widerstand entwickeln. Bei diesem gesteuerten Übergangswiderstand („transfer resistor“ oder besser Transistor) kann durch eine Strom der Widerstand verändert und so der durchgelassene Strom eingestellt werden.

Video-Transkript (Alternativ zur Erklärung im Video)

Schaltzeichen

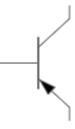
Abb. 1: Schaltzeichen und vereinfachter Aufbau von npn- und pnp-Bipolartransistors elektronische_schaltungstechnik:bipolartransistor_npn_oder_pnp_struktur.png

Wie gerade beschrieben, ist der Bipolartransistor durch eine dreilagige, abwechselnd dotierte Schichtstruktur aufgebaut, welche zwei entgegengesetzten und hintereinander geschalteten Dioden entspricht. Abhängig von der Schichtfolge (bzw. „Richtung der Dioden“) ergeben sich pnp- bzw. npn-Transistoren, die durch unterschiedliche Schaltzeichen mit drei Anschlüssen dargestellt werden (siehe Abbildung 1). Bei beiden Transistorvarianten werden vom Emitteranschluss (E) Ladungsträger Richtung Kollektoranschluss (C) ausgesandt, falls durch den Basisanschluss (B) ein geeigneter Strom fließt. Vereinfacht gesehen, könnten die negativen Ladungsträger der n-dotierten Seiten einen Strom durch eine NPN-Struktur darstellen, wenn auch in der p-dotierten Schicht negativen Ladungsträger vorhanden wären. Der damit fließende Strom $I_C$ in der technischen Stromrichtung wird im Schaltzeichen über die Pfeilrichtung am Emitter verbildlicht. Beim NPN-Transistor fließt also der Strom $I_C$ vom Kollektor zum Emitter. Da beim PNP-Transistor positive Ladungsträger die Leitfähigkeit ermöglichen, zeigt hier die technische Stromrichtung vom Emitter zum Kollektor und der Pfeil am Emitter zum Kollektor hin. Die Pfeilrichtung gleicht der Richtung der Diode bzw. des PN-Übergangs. Weitere Eselsbrücken zur Pfeilrichtung sind:

Korrekte Verschaltung der Transistoren

In der Simulation rechts ist die korrekte Verschaltung der Transistoren zu sehen. Allgemein muss bei der korrekten Verschaltung der Pfeil des Symbols der technischen Stromrichtung zeigen. Der Basisstrom $I_C$ wird in den Schaltungen fast immer durch eine Spannungsquelle zwischen Basis und Emitter mit einer Spannung $U_{BE}$ erzeugt. Dabei wird beim NPN-Transistor eine positive Spannung gegenüber des Emitters benötigt und beim PNP-Transistor eine negative Spannung gegenüber des Emitters. In der praktischen Anwendung überwiegen die NPN-Transistoren, unter anderem da die dort genutzten negativen Ladungsträger eine höhere Leitfähigkeit erzeugen. Für die folgenden Erklärungen werden nur NPN-Transistoren betrachtet.

Eine zentrale Frage die sich bei einem näheren Blick auf die Simulation rechts ergibt, ist: Warum muss beim NPN-Transistor ein technischer Strom in die Basis fließen, also positive Ladungsträger in die P-Schicht, zugeführt werden? Wäre es nicht einleuchtender, wenn die nicht vorhandenen und zum Transport benötigten negativen Ladungsträger zugeführt werden müssten?

Transistor im Bändermodell

Transistor im BändermodellAbb. 2: Transistor im Bändermodell

Um das zu verstehen, werden die Erkenntnisse des PN-Übergangs benötigt. Im Bild Abbildung 2 ist der Aufbau des NPN-Transistors im Bändermodell zu sehen. Im n-dotierten Kollektor und Emitter sind die frei beweglichen negativen Ladungsträger (blau) und ortsfesten positiven Ladungsträger (rot) eingezeichnet, in der Basis entsprechend die frei beweglichen positiven Ladungsträger (rot) und ortsfesten negativen Ladungsträger (blau). Beide PN-Übergänge haben eine Sperrschicht ausgebildet. Am Transistor liegt eine positive Spannung $U_{CE}$ an, welche in der dargestellten Situation keinen Stromfluss erzeugen kann. Durch die positive Spannung $U_{CE}$ und dem fehlenden Potential an der Basis sinkt die Spannung $U_{BE}$, was zu einer Verkleinerung der Sperrschicht führt. Im Gegensatz dazu erhöht sich die Spannung $U_{CB} = U_{CE} -U_{BE}$. Damit wird wird die Sperrschicht zwischen Basis und Kollektor größer. Bei Variation der äußeren Spannung $U_{CE}$ wird immer mindestens ein PN-Übergang vorhanden sein, der in Sperrrichtung verschalten ist, das heißt der Transistor sperrt.

Abb. 3: Funktion des npn-Bipolartransistors elektronische_schaltungstechnik:funktion_des_bipolartransistor2.png

Um die Sperrschicht zwischen Kollektor und Basis aufzuheben, muss diese in Durchlassrichtung verschaltet werden. Bis zum Durchschalten des Transistors sind dies mehrere Schritte, die im Folgenden über Abbildung 3 beschrieben werden:

  1. Bild: Die Physik dazu spielt sich in der schmalen p-Schicht ab. Die folgenden Bilder beziehen sich auf den markierten Ausschnitt.
  2. Bild - Situation $U_{CE}=0V, U_{BE}=0V$: In diesem Bild ist der unbestromte Transistor dargestellt. Darin sind die freien Ladungsträger (Elektronen in blau, Löcher in rot) und die Sperrschichten zwischen Basis und Emitter, sowie Basis und Kollektor in gelb. Nur der Sperrschicht sind die ortsfesten Ladungsträger mit deren Vorzeichen skizziert. Wie im Bändermodell dargestellt sind die ortsfesten Ladungsträger überall in beiden dotierten Bereichen vorhanden.
  3. Bild - Situation $U_{CE}=0V, 0V<U_{BE}<0,6V$: Zunächst soll eine kleine, positive Spannung $U_{BE}$ betrachtet werden. Dies stellt mit dem Strom $I_B$ Löcher in der Basis bereit. Dadurch wird der PN-Übergang zwischen Basis und Emitter in Durchlassrichtung betrieben. Im Bild ist mit schwarzen Kreisen angedeutet, dass die injizierten Löcher einige ortfeste negative Ladungsträger in beiden Sperrschichten kompensiert. Durch den Emitter fließen auch Elektronen in den n-Bereich nach, welche dort die Sperrschicht auf der anderen Seite abschwächen.
  4. Bild - Situation $U_{CE}=0V, U_{BE}>0,6V$: Wird die Durchlassspannung des PN-Übergang zwischen Basis und Emitter überschritten, so heben die injizierten Löcher und Elektronen die untere Sperrschicht auf. In der Simulation unten ist zu sehen, dass die Verschaltung des Transistors in der Art ist, dass in der (physikalisch nicht ganz korrekten) Diodenschaltung die Diode zwischen Basis und Emitter leitend wird.
  5. Bild - Situation $U_{CE}>0V, U_{BE}>0,6V$: Mit dieser Spannung an der Basis soll nun der Arbeitskreis, also am Ausgang eine Spannung $U_{BE}>0$ anliegen. Im realen System ist die Basis im Vergleich zur mittleren freien Weglänge der Elektronen („Weg bis zur Rekombination mit einem Loch“) sehr klein. Damit ändert sich die Situation am oberen PN-Übergang. In einer klassischen Diode sind im p-dotierten Bereich keine Elektronen vorhanden. Die aber hier vorhandenen Elektronen können die Basis durchschreiten und in der oberen Sperrschicht die ortfesten positiven Ladungsträger kompensieren. Die in die Basis injizierten Löcher wiederum kompensieren die ortfesten negativen Ladungsträger. Damit wird auch diese Sperrschicht abgebaut. Dies ist möglich solange genügend Löcher in die Basis eingebracht werden.
  6. Bild - Situation $U_{CE}>0V, U_{BE}>0,6V$: Beim NPN-Bipolartransistor tragen also sowohl Löcher (zum Aufheben der Sperrschichten), als auch Elektronen (als „Hauptverantwortliche“ für den Ladungstransport, die sog. Majoritätsträgerladungen) zur Leitfähigkeit bei. Daher rührt der Name Bipolartransistor.

Die Simulation rechts zeigt das vereinfachte Modell der entgegengesetzten Dioden. Der notwendige Eingangsstrom $I_C$ und die dazu entsprechende Eingangsspannung $U_{BE}$ gleicht den Verhältnissen der Diode zwischen Basis und Emitter. In Abbildung 4 ist ist das Funktionsprinzip dargestellt. Der Strom $I_B$ über die Diode zwischen Basis und Emitter regelt den Strom $I_C$ im Arbeitskreis. Diese Reglung geschieht über den veränderlichen Widerstand $R_{CE}$.

jbt_funktionsweise.jpgAbb. 4: Funktion des npn-Bipolartransistors

Kenngröße, Kennlinien, Kennfelder

Im vorherigen Kapitel 1 Grundlagen zu Verstärkern wurde bereits schon auf Kenngröße einer Blackbox eingegangen, dort speziell für einen Verstärker. Die Methodik kann hier auch angewandt werden. Im Video oben wurde bereits schon die erste Kenngröße beschrieben: Die Stromverstärkung $\beta=\frac{d I_C}{d I_B}$, bzw. in Form einer Grafik, die Stromsteuerkennlinie $I_C(I_B)$.1)

Eine weitere Kennlinie ist das Eingangskennlinienfeld $U_{BE}({I_B})$ bzw. als differentielle Kenngröße (=Steigung in der Kennlinie) der differentielle Eingangswiderstand $r_{BE}=\frac{d U_{BE}}{d I_B}$. Wie bereits beschrieben, gleicht der Aufbau zwischen Basis und Emitter einer Diode. Das Eingangskennlinienfeld gleicht dementsprechend dem einer Diode. Da der Stromfluss $I_B$ sehr klein ist (wenige Mikroampere oder kleiner), ist der Eingangswiderstand $r_{BE}$ groß.

Die folgende Simulation zeigt die Stromsteuerkennlinie $I_C(I_B)$ und Eingangskennlinie(nfeld) $U_{BE}({I_B})$ durch Variation von $U_{BE}$ (bzw. $I_B$).

Für die Beschreibung des Transistors ist das Ausgangskennlinienfeld $U_{CE}({I_C})$ und der darin als Steigung vorhandene differentielle Kollektor-Emitter-Widerstand $r_{CE}=\frac{U_{CE}}{I_C}$ besonders wichtig. Dieses ist in der folgenden Simulation für unterschiedliche Eingangsspannungen $U_{BE}$ (und damit unterschiedlichen Steuerströmen $I_B$) zu sehen. Das Ausgangskennlinienfeld lässt sich in verschiedene Bereiche unterteilen:

  1. Sperrbereich: bei geringen Eingangsspannungen $U_{BE}< 600mV$ wird die Sperrschicht nicht abgebaut. Entsprechend wird der gesamte Transistor nicht leitend. Im Ausgangskennlinienfeld ist dies dadurch zu sehen, dass bei positiver Ausgangsspannung $U_{CE}$ der Ausgangsstrom $I_C$ sehr klein wird. In diesem Fall entspricht der Transistor auf der Ausgangsseite einem hochohmigen Widerstand, bzw. einem offenen Schalter.
  2. Verstärkungsbereich (oder aktiver Bereich): bei größeren Eingangsspannungen $U_{BE}> 600mV$ wird die Sperrschicht abgebaut. Im Verstärkungsbereich verhält sich die Ausgangskennlinie wie eine Gerade. Der Ausgangsstrom $I_C$ ist damit nur noch abhängig von $I_B$, so wie dies über die Stromverstärkung $\beta=I_C/I_B$ definiert ist.
  3. Sättigungsbereich: Der Sättigungsbereich ist bei größeren Eingangsspannungen $U_{BE}> 600mV$ und nur geringer Ausgangsspannung $U_{CE}$ zu finden. Bei konstanter Eingangsspannung $U_{BE}$ verhält sich die Ausgangsspannung zum Ausgangsstrom wie ein hoher, nicht-linearer Widerstand. in diesem Fall entspricht der Transistor auf der Ausgangsseite einem niederohmigen Widerstand, bzw. einem leitenden Schalter.

Im Datenblatt ist gelegentlich eine andere Nomenklatur zu finden, die sich aus der sogenannten H-Charakteristik der Vierpoltheorie2) ergibt:

Der Bipolartransistor wird dort genutzt, wo eine geringe Schwellspannung oder ein Stromverstärker benötigt wird. Die ist beispielsweise bei verschiedenen Verstärkerschaltungen vorteilhaft. Auch in einigen einfachen Netzteilen sind Bipolartransistoren zu finden. Die häufigste Bipolartransistorschaltung ist die sogenannte Kollektorschaltung. Diese ist dadurch gekennzeichnet, dass am Kollektor eine konstante Spannung - die Versorgungsspannung - anliegt. Mehrere Kollektorschaltungen können durch eine gemeinsamen Spannungsversorgung betrieben werden. Damit liegt an allen Kollektoranschlüssen die gleiche Spannung an. Aufgrund der breiten Verwendung die Bipolartransistoren hatten, wird auch heute noch die gemeinsame Spannungsversorgung von elektronischen Schaltungen $V_{CC}$ genannt, wobei $CC$ für Common Collector steht. Dies ist häufig selbst dann noch zu sehen, wenn keine Bipolartransistoren mehr verwendet werden.

Ein großer Nachteil des Bipolartransistors ist, dass für das Schalten ein Steuerstrom benötigt wird. Besonders in digitalen Schaltungen, aber auch in der Leistungselektronik, ergibt sich dadurch eine nicht zu vernachlässigende Eingangsleistung $P=U_{BE}\cdot I_B$. Diese führt zu Verlusten und Abwärme, die bei der Leistungsversorgung und thermischen Auslegung berücksichtigt werden müssen. Aus diesem Grund werden in aktuellen Mikrocontrollern keine Bipolartransistoren mehr genutzt. In diesen Feldern wurde der Bipolartransistor durch den Feldeffekt-Transistor verdrängt.

Merke: Bipolartransistoren

Es gibt 2 verschiedene Arten von Bipolartransistoren. Diese unterscheiden sich in der Art der Schichtenaufbaus, bzw. der Majoritätsträgerladungen:

  • npn-Bipolartransistoren: Die hauptsächliche Leitung geschieht über Elektronen. Diese können ohne Strom $I_B$ über die Basis den p-dotierten Bereich nicht durchlaufen. Durch $I_B>0$ werden Löchern in die Basis eingebracht, welche Sperrschichten abbauen.
  • pnp-Bipolartransistoren: Die hauptsächliche Leitung geschieht über Löcher. Diese können ohne Strom $I_B$ über die Basis den n-dotierten Bereich nicht durchlaufen. Durch $I_B<0$ werden Elektronen in die Basis eingebracht, welche Sperrschichten abbauen.

Beim Bipolartransistor sind beide Ladungsträgertypen am Transport beteiligt.

2.7 Funktionsprinzip eines Feldeffekt-Transistors

mosfet-front-final-test_jpg_project-body.jpgAbb. 5: Funktion des MOSFETs

Abb. 6: FET Schaltsymbole elektronische_schaltungstechnik:fet_prinzip.png

Auch ein Feldeffekt-Transistor (FET) besteht aus zwei gegeneinander geschalteten Dioden, die eine gemeinsame n- bzw. p-Schicht besitzen. Die Leitfähigkeit des Feldeffekt-Transistors wird jedoch nicht durch das Anlegen einer Steuerstroms, sondern allein durch eine Steuerspannung erzeugt. Auch beim Bipolartransistor wurde der Steuerstrom durch eine Steuerspannung generiert. Der Steuerstrom muss jedoch zum Ansteuern des Bipolartransistors dauerhaft fließen, da die über die Basis eingetragenen Ladungsträger intern rekombinieren.

In Abbildung 6 ist ein spezieller Feldeffekt-Transistor gezeichnet, dem sogenannten „Metall-Oxid-Halbleiter Feldeffekt-Transistor“. Dieser soll im Folgenden näher erklärt werden. Die Abbildung 5 skizziert das Funktionsprinzip: Die Steuerspannung $U_{GS}$ (im englischen $V_{GS}$) regelt im Arbeitskreis den Strom $I_D$. Dies geschieht durch den Widerstand zwischen $R_{DS}$.

Um die Transistortypen zu unterscheiden, und die dahinterliegende Physik zu betonen, sind die Anschlüsse beim Feldeffekt-Transistor anders bezeichnet:

Daneben gibt es im Aufbau noch das „Bulk“ (B), was das Grundsubstrat des Transistors bezeichnet. Dies ist in der Regel nicht separat herausgeführt, sondern mit dem Sourceanschluss kurzgeschlossen. Bei einigen FETs ist das Bulk durch die mittlere Verbindung dargestellt.

In der Simulation rechts ist zu sehen, dass sich der Feldeffekt-Transistor so ähnlich wie ein Schalter verhält, welcher über eine Spannung gesteuert wird. Auf das Gate scheint kein Strom zu fließen, aber wenn sich die Spannung am Gate ändert, so ändert sich das Verhalten von „leitfähig“ in „offen“.

Metall-Oxid-Halbleiter Feldeffekt-Transistor (MOSFET)

Abb. 7: MOSFET Schichtung elektronische_schaltungstechnik:mosfet_pinch_off.png

Der Aufbau des Metall-Oxid-Halbleiter Feldeffekt-Transistors (englisch Metal Oxide Semiconductor Field Effect Transistor: MOSFET) ähnelt auf dem ersten Blick dem Bipolartransistor. In Abbildung 7 ist in den einzelnen Bildern (1)…(3) die Schichtung eines n-Kanal (englisch n-Channel) MOSFETs und in (4) nochmals das Schaltsymbol dargestellt. Im Gegensatz zum npn-Bipolartransistor ist hier aber mittlere p-dotierte Schicht (Bulk) nicht direkt an der Steuerelektrode angeschlossen. Vielmehr bildet die Metallschicht des Gates (Abbildung 7, Bild (5), grau), die Isolationsschicht des Oxids (im Bild violett) und die leitfähige, p-dotierte Schicht des Bulks (im Bild rot) einen Kondensator. Dabei ist zu beachten, dass das Bulk auf dem Potential des Source-Anschlusses liegt (gestichelte Linie im Bild).

Ohne Spannungsdifferenz $U_{GS}$ zwischen Gate und Source bildet sich an den p-n Übergängen eine (kleine) Sperrschicht aus. Wird die Spannungsdifferenz $U_{GS}$ vergrößert, so wird der Kondensator zwischen Gate und Bulk aufgeladen. Damit reichern sich gegenüber der Gatelektrode Elektronen an (Abbildung 7, Bild (2), dunkelblauer „Keil“). Übersteigt die Spannungsdifferenz $U_{GS}$ eine bestimmte Schwellspannung, so bilden die angereicherten Elektronen einen Kanal zwischen Source und Gate. Damit kann ein Strom $I_D \gg 0$ durch den MOSFET (Abbildung 7 Bild (3)) fließen.

Das Schaltsymbol (Abbildung 7, Bild (4)) lässt sich auch folgendermaßen beschreiben: Es bilden sich im ausgeschalteten Zustand jeweils Kondensatoren zwischen Gate und Source, zwischen Gate und Basis und zwischen Gate und Drain wegen der Oxidschicht (im Bild (1) violett) aus.3) Um den MOSFET anzusteuern, muss die Spannung am Gate $U_{GS}$ so geartet sein, dass sich ein PN-Übergang im Bulk bildet, angedeutet durch das weiß ausgefüllte Dreieck im Bild (4). Da die Spitze des Dreiecks (bzw. des damit skizzierten Diodensymbols) in Richtung des Gates zeigt, ist klar, dass es sich um einen n-Kanal MOSFET handelt.

In der Simulation rechts sind die gleichen Spannungsverhältnisse wie in Abbildung 7 (1)…(3) dargestellt. Durch den Wechselschalter links ist es möglich die Spannung $U_{DS}$ über den Transistor zu invertieren. Wird diese negativ, so stellt sich eine etwas andere Situation ein: Der MOSFET scheint leitfähig zu werden, unabhängig davon, welche Spannung $U_{GS}$ annimmt. Dies ist darauf zurückzuführen, dass sich im Schichtenaufbau eine weitere Diode versteckt hat: zwischen Bulk (p) und Drain (n) hat sich eine Sperrschicht ausgebildet, welche bei $U_{DS}<0$ und mit der Anbindung von Bulk und Source in Durchlassrichtung betrieben wird. Diese sogenannte Body-Diode ist in der Simulation bei (3b) explizit eingebaut.

Beim realen MOSFET als Bauteil begrenzt die Dicke des Kanals den Stromfluss. Um den maximalen Stromfluss zu erhöhen, wird der dargestellte Schichtaufbau mehrfach nebeneinandergelegt. Eine Variante davon ist der ist der HEXFET (Markenname von IR), welche in dieser Application Note zu finden ist.



Ausgangskennlinienfeld des MOSFET

Auch beim MOSFET soll das Ausgangskennlinienfeld $U_{DS}({I_D})$ betrachtet werden. Auch dieses ähnelt dem Bipolartransistor, jedoch sind nun die verschiedenen Kennlinien durch unterschiedliche Steuerspannungen $U_{GS}$ und nicht durch einen Steuerstrom einstellbar.

Leider unterscheidet sich die Benennung der verschiedenen Betriebsbereiche eines MOSFETs von denen des Bipolartransistors:

  1. Sperrbereich: bei geringen Eingangsspannungen $U_{GS}$ kann kein Kanal gebildet werden. Entsprechend wird der gesamte Transistor nicht leitend. Im Ausgangskennlinienfeld ist dies dadurch zu sehen, dass bei positiver Ausgangsspannung $U_{DS}$ der Ausgangsstrom $I_D$ sehr klein wird. In diesem Fall entspricht der Transistor auf der Ausgangsseite einem hochohmigen Widerstand, bzw. einem offenen Schalter.
  2. Sättigungsbereich: bei größeren Eingangsspannungen $U_{GS}> U_{th}$ oberhalb eines Grenzwerts (engl. Threshold) wird ein leitfähiger Kanal gebildet. Im Sättigungsbereich verhält sich die Ausgangskennlinie wie eine Gerade. Der Ausgangsstrom $I_D$ ist damit nur noch abhängig von $U_{GS}$.
  3. linearer Bereich (aktiver Bereich) : Der lineare Bereich ist bei größeren Eingangsspannungen $U_{GS}> U_{th}$ und nur geringer Ausgangsspannung $U_{DS}$ zu finden. Bei konstanter Eingangsspannung $U_{GS}$ verhält sich die Ausgangsspannung zum Ausgangsstrom wie ein hoher, nicht-linearer Widerstand. In diesem Fall entspricht der Transistor auf der Ausgangsseite einem niederohmigen Widerstand, bzw. einem leitenden Schalter.

Zu beachten ist, dass der Sättigungsbereich bei MOSFET und Bipolartransistor unterschiedliche Arbeitsbereiche kennzeichnet.

Varianten von MOSFETs


Abb. 8: FET Schaltsymbole elektronische_schaltungstechnik:fet_schaltsymbol.png

Der bisher betrachtete (und auch am häufigsten genutzte) Feldeffekt-Transistor ist der sogenannte „n-Kanal Anreicherungstyp MOSFET“. Dabei rührt der Teil „n-Kanal“ vom Typ des Strom-bildenden Ladungsträgers und wurde bereits weiter oben gegeben. Der Teil „Anreicherungstyp“ (engl. enhancement) stellt dar, dass die Ladungsträger zunächst nicht vorhanden sind und zur Leitfähigkeit erst mittels des der Spannung $U_{GS}$ im Bulk angehäuft werden müssen.

Bei einigen Schaltungen (insbesondere Digitalschaltungen) werden auch „p-Kanal Anreicherungstyp MOSFET“ verwendet, bei dem Löcher die Strom-bildenden Ladungsträger sind. In der Simulation rechts ist diese Art des MOSFET gezeigt. Am deutlichsten ist, dass bei der Verschaltung des p-Kanal Anreicherungstyp MOSFET in der Regel Drain und Source vertauscht wird. Damit werden die Zahlenwerte von $U_{DS}$ und $I_D$ im Ausgangskennlinienfeld negativ. Um Löcher im p-Kanal anzureichern muss eine negative Spannung am Gate $U_{DS}<0$ anliegen.

In der Abbildung 8 sind die Schaltsymbole verschiedener Varianten von MOSFETs dargestellt. In den MOSFETs der oberen Zeile wird ein n-Kanal zum Ladungstransport ausgebildet, in der unteren ein p-Kanal.

In Abbildung 8 links oben sind drei Varianten eines n-Kanal Anreicherungstyp MOSFET gezeigt. Beim ersten Schaltsymbol stellt der Kreis dar, dass es sich um ein diskretes Bauteil handelt, also ein einzelnen MOSFET, der nicht mit anderen gemeinsam in einem Chip integriert ist. Das zweite Schaltsymbol wurde bereits in den vorherigen Kapitel genutzt. Das dritte Schaltsymbol des gleichen n-Kanal Anreicherungstyp MOSFET ist die reduzierte Variante (also ohne Bulk). Diese Darstellung wird zur Vereinfachung in Digitalschaltungen genutzt.

In Abbildung 8 links unten sind drei Varianten eines p-Kanal Anreicherungstyp MOSFET gezeigt. Auch hier zeigt der Kreis beim ersten Schaltsymbol an, dass es ein diskretes Bauteil ist, jedoch ist nun die die Pfeilrichtung am Bulk gedreht. Das zweite Schaltsymbol wird - wie beim n-Kanal MOSFET - so auch in integrierten Schaltungen verwendet. Das dritte Schaltsymbol ist wieder die reduzierte Variante (also ohne Bulk). Für die Digitalschaltung ist nur wichtig, ob der Schalter bei High-Signal ($= 5V$) schließt oder öffnet. Da der p-Kanal Anreicherungstyp MOSFET öffnet, wird dieser mit einem Negierungszeichen (kleiner Kreis) am Gate gezeichnet.

In Abbildung 8 rechts sind sogenannte n-Kanal und p-Kanal Verarmungstyp MOSFET dargestellt. Die bisherig betrachteten MOSFETs waren im ausgeschalteten Zustand (also $U_{DS}=0$) nicht leitfähig. In manchen Anwendungen wäre es aber gut, wenn der MOSFET im ausgeschalteten Zustand einem leitfähigen Schalter gleicht. Mit Blick auf die Schichtstruktur (Abbildung 7, Bild (1)…(3)) ist dies über eine gezielte Umdotierung des Bereichs gegenüber des Gates möglich. Durch die Dotierung kann ein leitfähiger Kanal verstellt werden. Die Ladungsträger dieses Kanals können durch ein geeignetes Feld - und damit geeignete Gatespannung $U_{GS}$ - verdrängt bzw. verarmt werden. Damit wird der MOSFET bei einer Gegenspannung $U_{GS}$ nicht-leitend. Im Schaltsymbol ist der „Kurzschluss“ zwischen Source und Drain auch bildlich eingezeichnet.

Merke: MOSFETs

Es gibt 4 verschiedene Arten von MOSFETs. Diese unterscheiden sich einerseits in der Art der Strom-bildenden Ladungsträger:

  • n-Kanal: Die Strom-bildenden Ladungsträger sind Elektronen.
  • p-Kanal: Die Strom-bildenden Ladungsträger sind Löcher.

Das zweite Unterscheidungsmerkmal ist die Leitfähigkeit im ausgeschalteten Zustand ($U_{GS}=0$):

  • Anreicherungstyp: Bei einer Gatespannung von $U_{GS}=0$, ist kein leitfähiger Kanal vorhanden. Erst durch das Aufladen des Gate-Bulk-Kondensators wird der Kanal gebildet bzw. die Ladungsträger angereichert.
  • Verarmungstyp: Bei einer Gatespannung von $U_{GS}=0$, ist ein leitfähiger Kanal vorhanden. Durch das Aufladen des Gate-Bulk-Kondensators wird der Kanal verkleinert bzw. die Ladungsträger verdrängt („verarmt“).

Beim Feldeffekttransistor werden durch das elektrische Feld des Gate-Bulk-Kondensators nur genau diejenigen Ladungsträger angereichert bzw. verarmt, welche zum Ladungstransport beitragen.

Abb. 9: Arbeitsbereich von Halbleiter-Elementen elektronische_schaltungstechnik:arbeitsbereich_von_halbleiterelementen.png

Auslegung von Halbleiter-Elementen

Bei allen Transistoren und Dioden sind für die Schaltungsauslegung verschiedene die Grenzwerte zu beachten. Diese können im Ausgangskennlinienfeld direkt eingetragen werden (Abbildung 9, oben). Durch die Erwärmung des Bauteils und der daraus steigenden Eigenleitung ergeben sich zwei Grenzwerte:

  • Im leitenden Zustand bildet die Verlustleistung $P_{loss}=R(T)\cdot I^2$ einen direkten Bezug zum Strom durch das Halbleiterelement $I_C, I_D, I_D$ (Bipolartransistor, MOSFET, Diode). Daraus ergibt sich Strom ein $I_{max}$, welcher nicht überschritten werden soll.
  • Im Zustand, bei dem sowohl ein merklicher Strom als auch eine merkliche Spannung anliegt, ergibt sich eine maximal erlaubte Leistung $P_{tot}=const.=U\cdot I$. Dies ist in der Ausgangskennlinie eine Hyperbel. Überschreitet der Ausgangsstrom diese Hyperbel, so erwärmt sich das Halbleiterelement so stark, dass durch die ansteigende Eigenleitung, die Leitfähigkeit absinkt, was wiederum zu einem steigenden Strom führt. Dieser Effekt führt zur thermischen Zerstörung der Komponente.

Daneben darf eine maximale Spannung $U_{max}$ nicht überschritten werden. Diese ist in meist auf die (interne) Durchschlagsfestigkeit des Bauteils zurückzuführen.

Diese Grenzen sind insbesondere dann wichtig, wenn z.B. ein MOSFET als Schalter genutzt werden soll (Beispiel: Abbildung 9, unten). In diesem Fall gibt es zwei Zustände:

  • Schalter ist leitfähig: Es liegt eine eine geringe Spannung $U_{DS}$ an, bei dem ein großer Strom $I_D<I_{max}$ fließt.
  • Schalter ist nicht leitfähig: Es liegt eine eine hohe Spannung $U_{DS}<U_{max}$ an, bei dem kein Strom fließt.

Beim Umschalten von „leitfähig“ nach „nicht leitfähig“ kann dabei - selbst, wenn die einzelnen Strom- und Spannungsgrenzen berücksichtigt werden - der Schalter zerstört werden. In Abbildung 9 ist dieser Fall im unteren Diagramm zu sehen. Der Stromfluss $I_D$ wird zunächst aufrecht erhalten (bzw. sind nur gering), obwohl Spannung $U_{DS}$ ansteigt (blaue Linie). In diesem Fall kann es dazu kommen, dass $P_{tot}$ überschritten wird und der MOSFET wegen thermischer Überlastung zerstört wird.

Um den Umschaltprozess (insbesondere bei Leistungs-MOSFETs, z.B. für Motortreiber) zu beschleunigen, erzeugen sogenannte Treiberschaltungen die Spannung $U_{GS}$. Mit diesen Treiberschaltungen kann die Steuerspannung sehr schnell bereit- und zurückgestellt werden. Dazu müssen für das Auf- und Entladen des Gatekondensator kurzfristig Ströme im Bereich von einigen Ampere bereitgestellt werden.

Merke: Maximale Ausgangswerte eines Halbleiterelements

Bei jedem Halbleiterelement sind am Ausgang drei Maximalwerte zu beachten:

  • einer maximalen Spannungsgrenze $U_{max}$,
  • einer maximalen Stromgrenze $I_{max}$,
  • einer maximalen Leistungsgrenze $P_{tot}=U \cdot I$

2.8 Anwendungen für Bipolartransistoren

Darlington-Transistor

Die Darlington-Schaltung bzw. der Darlington-Transistor (als diskretes Element) ist ein einfacher Aufbau, welcher es ermöglicht mit erheblich geringerem Basisstrom $I_B$ die Ausgangsspannung $U_{BE}$ zu steuern. Rechts ist die Darlington-Schaltung im Vergleich zu einem einfachen Bipolartransistor zu sehen. Details sind in Wikipedia unter Darlington-Schaltung zu finden.

Innenleben eines Operationsverstärkers

Der Operationsverstärker als „fast idealer“ Differenzspannungsverstärker stellt ab dem nächsten Kapitel eine zentrale Komponente der elektronischen Schaltungstechnik dar. Im Kapitel Grundlagen zu Verstärkern - Rückkopplung wurde bereits ein idealer Differenzspannungsverstärker genutzt. In der Simulation rechts ist der Kern des Differenzspannungsverstärker vereinfacht dargestellt. Dementsprechend ist auch keine Differenzspannung am Eingang zu sehen, sondern eine kleine sinusförmige Spannung. Diese liegt zunächst an der Basis des ersten Bipolartransistor, welche eine hochohmige Eingangsverstärkerstufe darstellt. Der dadurch geregelte Strom $I_C$ führt wiederum auf eine Basis eines weiteren Bipolartransistors und danach auf die Ausgangsverstärkerstufe. In der Simulation erreicht dieser Aufbau eine Differenzverstärkung von etwa $A_D=10'000'000$. In realen Differenzspannungsverstärker liegt dieser eher im Bereich $A_D ≈100'000$. Details sind in Wikipedia unter Operationsverstärker zu finden.

2.9 Anwendungen für Feldeffekttransistoren

NOT Gatter

So gut wie alle Consumer-Elektronik Produkte sind im Kern aus Feldeffekttransistoren aufgebaut. In Detail wird dabei auf die CMOS-Technologie (CMOS: Complementary metal-oxide-semiconductor) zurückgegriffen. Dabei verhalten sich die MOSFETs auf der Seite zu Masse und die MOSFETs auf der Seite zur Spannungsversorgung gerade gegensätzlich, also komplementär. In der Simulation rechts ist das einfachste Gatter, das NOT-Gatter, dargestellt. Ein weiteres Gatter wurde einführend betrachtet.

Verpolschutz

Viele Chips (wie z.B. Microcontroller) können durch eine falsch gepolte Spannungsversorgung zerstört werden. Eine batteriebetriebene Elektronik sollte dafür eine aktive Schutzschaltung haben. Eine Diode ist bei der Spannungsversorgung nicht praktikabel (warum?). Stattdessen kann ein MOSFET genutzt werden, der negative Spannungen nicht durchlässt. Details sind auf der Seite von Lothar Miller gut erklärt.

Pegelwandler

Bei der Elektronikentwicklung kann es vorkommen, dass mehrere integrierte Schaltkreise (z.B. intelligenter Lichtsensor, Mikrocontroller, intelligente LED) unterschiedliche Spannungsniveaus benötigen. Dies kann insbesondere beim Datenaustausch zu Problemen führen, wenn logic High in einem bestimmte Spannungsbereich liegen muss. Dieses Problem kann ein Pegelwandler lösen. Der Pegelwandler (auch Logic Level Converter, Level Shifter) ermöglicht die bidirektionale Verbindung von digitalen Anschlüssen unterschiedlicher Spannungsniveaus, z.B. 5 V auf 3,3 V.

Für den Levelconverter kann jeder n-Kanal enhancement MOSFET genutzt werden, dessen Schwellspannung unter $1,8…2,0 V$ liegt. Diese Grenze ist auf den Mindestlogikpegel von $2,0 V$ für logisch High zurückzuführen. Der Einfachheit halber werden „logic level enhancement mode MOSFET“ eingesetzt, welche gerade für die Logikspannung von $3,3V$ optimiert sind.

Die Funktionsweise ist auf Wikipedia gut erklärt und kann sich mit der Simulation hergeleitet werden.

Spannungsverdoppler/-invertierer

Als Energieversorgung für Elektronik wird häufig $5V$ oder $3,3V$ verwendet. Im folgenden Kapitel werden wir sehen, dass für Operationsverstärkerschaltungen häufig eine bipolare Spannungsversorgung genutzt wird. Um aus einer Versorgung mit $5V$ auch $-5V$ bei geringen Strömen erzeugen zu können, werden häufig Ladungspumpen genutzt. Eine solche ist rechts in der Simulation zu sehen. Im Oszilloskop (in der Simulation unten) wird die Spannung $U_{C1}$ am Eingangskondensator C1 und $U_{C2}$ am Speicherkondensator C1 angezeigt. Diese Schaltung ist z.B. im IC ICL7660 (Renesas), LMC7660 (TI), TC7660 (Microchip) integriert. Details zur Funktionsweise sind z.B. in diesem Video zu finden.

Lernfragen:

  • In welchem Zustand ist die Spannung $U_{C1}$ gleich $1 V$?
    In welchem Zustand ist die Differenz der Spannungen $U_{C2}-U_{C1}$ an den beiden Kondensatoren gleich $1V$?
  • Was passiert, wenn die Spannungsquellen für $0V$ und $1V$ vertauscht werden?
  • Wie lässt sich diese Schaltung statt mit Wechselschaltern mit Dioden realisieren?

Spannungsinvertierer im Mikrocontroller

In manchen Mikrocontrollern wird intern eine negative Spannung (z.B. für Operationsverstärker) benötigt. Da diese Spannung nicht von außen zugeführt wird, muss der Mikrocontroller diese über eine interne Schaltung bereitstellen. In der Simulation rechts ist eine Schaltung dargestellt, die so in einen Mikrocontroller integrierbar ist. Der Ringoszillator generiert dabei eine hochfrequentes Taktsignal, welches eine Inverterstufe (logisches NOT-Gatter) ansteuert. Über die beiden Kondensatoren kann dann die Ladung so heruntergeschaufelt werden, dass der Kondensator am Ausgang eine negative Spannung bereitstellt. Weiterführende Informationen sind in Wikipedia unter Ladungspumpe und unter „Inside the 8087's substrate bias circuit“ zu finden.

Step-Down-Converter

Bisher wurde eine Spannungserhöhung über das gepulste Laden von Kondensatoren beschrieben. Es gibt auch Anwendungen, bei denen Leistung von einer höherer Spannung auf eine geringere Spannung transferiert werden muss. Ein Beispiel hierbei ist ein System mit einem Microcontroller, welcher $5V$ benötigt um schnell rechnen zu können und einem Sensor, welcher mit $3.3V$ versorgt werden muss. Eine Lösung dafür ist die Verwendung einer Halbbrücke und einem Tiefpassfilter 2. Ordnung (LC-Filter). Diese Schaltung wird Tiefsetzsteller (engl. Step-Down-Converter oder Buck-Converter) genannt. Für die praktische Anwendung gibt es ICs (z.B. die AP62xxx-Reihe oder DIO6012B) in denen bereits die Leistungselektronik (Transistoren) mit der Steuerelektronik verbaut ist. Es müssen für eine Anwendung nur noch die Passivkomponenten (Widerstände, Kondensatoren, Induktivitäten) ausgelegt werden.

Lernfragen:

  • Warum kann hier nicht einfach ein Spannungsteiler genutzt werden?
  • Warum wird kein RC- oder RL-Filter genutzt?

Vierquadrantensteller

Bei vielen Anwendungen müssen Strom und Spannung unabhängig voneinander gesteuert werden. Dies ist beispielsweise bei einem Motor (= ohmsch-induktive Last) der Fall. Dort ist der Strom im wesentlichen proportional zum Drehmoment und die Spannung von der Drehzahl. Sollen hierbei Spannung und Strom bipolar ausgegeben werden (bzw. in der Anwendung: Drehmoment und Drehzahl in beide Richtungen geregelt werden), so bietet sich ein Vierquadrantensteller aus Transistoren an. In modernen integrierten Schaltkreisen sind diese aus MOSFETs aufgebaut, direkt mit dem MOSFET-Treiber versehen und mehrere Vierquadrantensteller nebeneinander zu finden (z.B. dem SchrittmotortreiberDRV8835). Details sind auf Wikipedia unter Vierquadrantensteller zu finden.

Rückkoppelschaltungen mit Transistoren

Mit zwei Transistoren kann eine sogenannte Astabile Kippstufe erstellt werden (siehe folgende Schaltung). Bei dieser sind zunächst beide Kondensatoren entladen. Um die Schaltung zu verstehen wurde durch den offenen Schalter $S$ die Kopplung beider Teile der Schaltung getrennt. Wird nun die Simulation gestartet, so geschieht diese Abfolge:

  1. Es fließt ein Basis-Strom $I_B$ über $Q1$, da $U_{BE}$ im Bereich $0.6V$ liegt.
  2. Damit wird $C2$ auf ca. $5V-0.6V$ aufgeladen.
  3. In dieser Situation nähert sich die Spannung am Knoten $K2$ $5V$ und am Knoten $K1$ $0V$.
  4. $C1$ ist damit auf $5V$ aufgeladen.

Wird nun der Schalter $S$, dann stellt der Kondensator $C1$ Strom für die Basis von $Q2$ bereit. Damit schaltet $Q2$ durch, womit die Spannung in Knoten $K2$ abrupt fällt. Durch den aufgeladene Kondensator $C2$ wird damit auch die Spannung an der Basis von $Q1$ nach unten gezogen, womit der Transistor $Q1$ öffnet. Damit sind nun die Situationen 1. und 2. in der obigen Abfolge für den Transistor $Q2$ wahr. D.h. die Situation hat sich gerade umgedreht. Da jeweils durch den durchgeschalteten Transistor dessen Kondensator an der Basis entladen wird und der entgegengesetzte aufgeladen wird, wechseln sich die Transistoren beim Durchschalten ab.

Diese eher abstrakte Schaltung hat diverse Anwendungen. Eine besondere ist in der folgenden Simulation dargestellt und wird gelegentlich im Internet referenziert (z.B. auf Mikrocontroller.net. Hierbei handelt es sich um eine Schaltung, mit welcher per Ultraschallsender und -empfänger der Abstand zu einem Ultraschall-reflektierenden Gegenstand ermittelt werden kann. Auf der linken Seite ist der Ultraschall-Empfänger zu sehen, welcher über einen Schwingkreis repräsentiert werden kann. Gleiches gilt für den Empfänger auf der rechten Seite. Beide Transistoren sind durch einen Kondensator verbunden, dessen eines Potential über ein Potentiometer eingestellt werden kann (siehe auch Slider „Spannungsteiler“). Zunächst scheint die Schaltung nicht vollständig mit der obigen Schaltung übereinzustimmen. Jedoch gibt der Sender auch Energie an den Empfänger und koppelt so mit diesem. Damit wirkt auch wieder eine Gegenkopplung - in der Simulation kann über das Schließen des Schalters $S$ die Kopplung aktiviert werden. Hinweis: Die Kopplung über Luft, Sender und Empfänger sind nur rudimentär umgesetzt (speziell die Übertragung, Dämpfung und die Impedanzen von Sender und Empfänger).

Weiterführendes

realer Aufbau von (Bipolar)Transistoren

Die konzeptionelle Darstellung eines modernen Bipolartransistors ist z.B. in diesem Skript der University of Tennessee zu sehen. Dort ist in der Skizze eine einzelne Transistorzelle abgebildet, welche durch sog. Trenches (zu deutsch Graben) abgetrennt ist. Ein Querschnitt eines realen Transistor ist in diesem Paper des Leibniz Institut zu finden.

Typische Vertreter von Bipolartransistoren sind BC857 (PNP) und BC846 (NPN).

Weitere MOSFET Anwendungen

MOSFETs werden nicht nur zum reinen Schalten von Strömen genutzt. Weitere Anwendungen sind auch:

  1. als Anzeige-Element in TFT-Bildschirmen (TFT ... Thin Film Transistor)
  2. als Speicherelement z.B. in SD-Karten (Floating-Gate-Transistor, oder auch neue Ansätze, wie Ferroelectric_Random_Access_Memory)
  3. als integriertes „Vorschaltelement“ für Leistungs-Bipolartransistoren, speziell im Bipolartransistor_mit_isolierter_Gate-Elektrode (IGBT)
  4. als chemischer Sensor für diverse Materialien (siehe Chemisch_sensitiver_Feldeffekttransistor)
  5. als Bindeglied zwischen Photonik/Optoelektronik und klassischer Elektronik

Andere Arten von elektronischen Schaltern

Um größere Ströme steuern zu können werden häufig MOSFET und Bipolartransistor kombiniert: der Bipolartransistor kann dabei die großen Ströme schalten und der MOSFET stellt den Steuerstrom für den Bipolartransistor bereit. Prinzipiell ähnelt die Schaltung dann einem Darlingtontransistor, bei dem ein MOSFET einen Bipolartransistor steuert. In der praktischen Umsetzung sind beide Transistoren auf dem gleichen Substrat ineinander verschachtelt. Dieser Transistortyp wird IGBT genannt. Einige Automobilhersteller nutzen diesen in Elektrofahrzeugen zur Wandlung der Batterie-Gleichspannung in eine Wechselspannung für den Motor. Dazu werden Halbbrücken verwendet; ein Beispiel für eine solche ist die von Bosch entwickelte IGBT-Halbbrücke:

Neben den IGBTs kommen mit neuen Materialien wie GalliumNitrid und Siliciumcarbid auch neue Komponenten in den Fokus. Dabei wird der MOSFET zum Metall-Halbleiter-Feldeffekttransistor (MESFET) abgewandelt: Bei diesem wird ein leitfähiger Bereich (Kanal) durch eine Sperrschicht eingeschnürt. Die Sperrschicht entsteht hier direkt durch Kontakt des metallischen Gate Anschlusses mit dem Halbleiter. Der Kontakt entspricht gerade einer Schottky-Diode. In der Praxis wird das Konzept zum High-electron-mobility transistor weiterentwickelt, da diese sowohl hohe Spannungsfestigkeit, als auch hohe Stromtragfähigkeit versprechen.

Übungen

Aufgabe 2.8.1: Strom-/Spannungs-/Leistungsbegrenzung

Stellen Sie sich von, Sie arbeiten in der Firma „Mechatronics and Robotics“ und versichen ein IoT Gerät für Fahrzeuge zu entwickeln.
Dieses Gerät soll die Energie aus einer $12V$-Batterie beziehen um zyklisch Informantionen über WLAN zu übermitteln. Der WLAN Chip benötigt $3.3V$ Versorgungsspannung und zieht bis zu $800mA$ an Strom sobald er Daten überträgt.

Für die Versorgung soll ein Linearregler genutzt werden. Konkret soll ein LM317 Regler verwendet werden. Ein Linearregler agiert als geregelter Widerstand, welcher seinen Spannungsabfall gerade so einregelt, dass eine vorgegebene, konstante Spannung an seinem Ausgang entsteht. Diese Ausgangsspannung kann über einen Spannungsteiler eingestellt werden.

  1. Analysieren Sie das LM317 Datenblatt um herauszufinden, ob der LM317 für folgenden Arbeitspunkt geeignet ist:
    1. Eingangsspannung $V_{I,max}=14V$,
    2. Ausgangspannung $V_{O}=3.3V$ und
    3. Ausgansstrom $I_O=0.8A$.
  2. Wenn der Linearregler als Vorwiderstand agiert: wie kann dann die Verlustleistung $P_{loss}$ berechnet werden?
  3. Durch die Verlustleistung $P_{loss}$ steigt die Temperatur des ICs. Die Verlustleistung wird sich im PN-Übergang generiert. Dadurch entsteht ein Temperaturgefälle $T_{Jx}$ zwischen dem Übergang (engl. junction) und der Umgebung. Der IC wird auf eine Platine gelötet, entsprechend ist das Temperaturgefälle $T_{JB}$ zwischen Übergang und der Platine (engl. Board) hier am wichtigsten. Dieses Temperaturgefälle kann wiefolgt berechnet werden: $\Delta T_{JB}= T_{J} - T_{B} =R_{\theta JB}\cdot P_{loss}$, wobei $R_{\theta JB}$ der thermischen Widerstand (= Hemmung des Wärmeflusses) zwischen PN-Übergang und der Platine darstellt.
    1. Suchen Sie die thermischen Informationen des LM317 in im Datenblatt und berechnen Sie die maximale Temperatur des PN-Übergangs $T_{J}$, wenn die Platinentemperatur $T_{B}=30°C$ vorgegeben ist.
    2. Welcher Chipgehäusetype (engl. package) des ICs kann genutzt werden, damit die Betriebstemperatur am PN-Übergang $T_J$ nicht über die empfohlenen Betriebsbedingungen (engl. recommended operating condition, siehe Datenblatt) hinausläuft?

Aufgabe 2.10.1: Betafaktor eines BJT

  1. Ein Bipolartransistor (engl. bipolar junction transitor, BJT) regelt den Strom durch eine Last. Es ergibt sich ein Kollektorstrom $I_C = 398 mA$ und ein Basisstrom $I_B= 2 mA$. Welchen Wert hat die Stromverstärkung $\beta$?
  2. Ein häufig genutzter Bipolartransistor ist der BC847, welcher von verschiedenen Herstellern gekauft werden kann. Es soll das Datenblatt BC847 - Nexperia verwendet werden. Was ist der benötigte Basisstrom $I_B$, wenn ein Kollektorstrom $I_C=2mA$ über den Transistor fließen soll? Berechnen Sie $I_B$ für alle 3 Arten des BC847 Transistors im Datenblatt.

Aufgabe 2.10.2: Spannungsberechnung

Es soll untenstehende Schaltung (zunächst mit den darin angegebenen Werten) gegeben sein.

  1. In Fall $1$ ist der Basisstrom mit $I_{B,1}=50\mu A$ und die Stromverstärkung $\beta_1=150$ gegeben.
    Berechnen Sie den Spannungsabfall $U_{L,1}$ an der Last $R_L$ und die Spannung $U_{CE,1}$.
  2. Im Fall $2$ wird ein Basisstrom $I_{B,2}=250\mu A$ benötigt.
    1. Berechnen Sie dafür als erstes $U_{BE,1}$ in der ersten Situation. $U_{BE}$ wird nun als konstant angenommen ($U_{BE}=U_{BE,1}=U_{BE,2}$).
    2. Berechnen Sie den benötigten Wert für $R_{B,2}$.
    3. Starten Sie die Simulation und setzen Sie $R_B$ zu dem berechneten Wert. Versuchen Sie $\beta_2$ zu ermitteln. Warum ist dies nun nicht mehr gleich $\beta_1 = 150$?

Aufgabe 2.10.3: Low Side Switch und High Side Switch

Es sei die Schaltung in der Simulation unten gegeben. Die Transistoren hier werden „High Side Switch“ bzw. „Low Side Switch“ genannt, abhängig von der Spannung zu welcher diese schalten können. In den dargestellten Schaltungen kann jeder Transistor jeweils den Strom über einen Lastwiderstand von $10\Omega$ steuern. Als Eingangsspannung zur Basis / Gate soll ein logisches Signal mit den Spannungsniveaus von $0V$ und $5V$ genutzt werden.

  1. Erklären Sie die Vorteile von MOSFET im Vergleich zu Bipolartransistoren anhand dieser Anwendung.
  2. Ädern Sie die Spannung $VCC$ von $5V$ zu $15V$ durch den Schalter in der unteren linken Ecke. Sind die Transistoren immernoch fähig in allen Konfiguationen zwischen Kurzschluss und offener Leitung hin und her zu schalten?
  3. Wie könnte dieses Problem gelöst werden? Versuchen Sie die Bipolarschaltung des Low Side Switch als Treiberschaltung für den FET High Side Switch zu nutzen. Erweitern Sie dazu die Schaltung in der Simulation.

Aufgabe 2.10.4: Einfacher Temperaturdetektor

Es soll die Schaltung unten gegeben sein. $R_2$ ist ein NTC Widerstand, der als Sensor das Überschreiten einer Grenztemperatur detektierbar machen soll. In der Schaltung kann die Temperatur über den Regler Temperature rechts geändert werden.

  1. Als Erstes soll der Reihenwiderstand vor der LED berechnet werden. Dazu kann der Spannungsabfall $U_{CE}$ am Bipolartransistor zunächst vernachlässigt werden. Die LED soll bei $10mA$ hell leuchten (das Leuchten startet etwa bei $1mA$). Die Versorgungsspannung sei $U_S=5.0V$ und die Kniespannung der LED $U_{LED}=1.7V$.
    1. Was ist der ideale Wert für $R_D$?
    2. In der Simulation ist der Wert nicht korrekt. Welchen Effekt hat dies?
  2. Als Zweites soll das System für einen Detektion der Grenztemperatur von $T_0=50°C$ konzeptioniert werden.
    1. Die $R(T)$-Kennlinie des NTC $R_2$ ist im Diagramm unten dargestellt. Was ist der Wert von $R_2(T_0)$?
    2. Der Bipolartransistor soll für $U_{BC}=0.6V$ voll leitfähig sein. Welchen Wert muss $R_1$ haben?

elektronische_schaltungstechnik:diagramtemperaturesensor.png

Lernfragen

zum Selbststudium

  • Beschreiben sie die Funktion eines Transistors
    • Skizzieren Sie den Schichtenaufbau eines Bipolartransistors. Erklären Sie das Durchschalten eines PNP-Bipolartransistors mit Hilfe der gezeichneten Skizze.
    • Zeichnen sie das vereinfachte Dioden-Ersatzschaltbild eines NPN Transistors beschreiben Sie die Funktionsweise.
  • Erklären Sie den Unterschied zwischen einem PNP und NPN Transistor.
    • Zeichen Sie jeweils eine Schaltung, bei dem der jeweilige Schalter an U+ = 5V und Masse so angeschlossen ist, dass ein Durchschalten mit einer Spannung zwischen U+ und Masse an der Basis möglich ist.
    • Benennen Sie die jeweiligen Anschlüsse der Transistoren in der Zeichnung.
    • Welche Spannung muss jeweils an der Basis angelegt werden, damit der Transistor durchschaltet?
    • Wie ist jeweils das Vorzeichen des Steuerstroms zu wählen?
    • In welchem Größenbereich liegt eine typische Stromverstärkung?
  • stromgesteuerte und spannungsgesteuerte Transistoren
    • Erläutern Sie den Unterschied zwischen einem stromgesteuerten und einem spannungsgesteuerten Transistor.
    • Welche Transistorart ist stromgesteuert, welche spannungsgesteuert?
    • Zeichnen Sie jeweils ein Schaltzeichen für einen stromgesteuerten und einen spannungsgesteuerten Transistor.
    • Wie ist die Reihenfolge der Dotierung der gezeichneten Transistoren?
  • Welche zwei grundlegenden Typen von Transistoren gibt es?
  • MOSFET
    • Welche Vorteile hat ein MOSFET gegenüber einem Bipolartransistor?
    • Wie ist ein MOSFET aufgebaut? (Schichtstruktur, Anschlüsse)
  • H-Brücke
    • Zeichnen Sie eine H-Brücke mit Schaltern (idealer Schalter), einer ohmsch/induktiven Last und einer externen Spannungsquelle mit V+ und GND.
    • Wie können die verschiedenen Schalter angesteuert werden, um eine beliebige Spannung zwischen V+ und V- an der Last anliegen zu haben? Was ist der Fachausdruck für die Ansteuerungsart?
  • Zeichnen Sie das notwendige PWM-Signal, um bei einer Vollbrücke eine sinusförmige Ausgabe zu generieren.
  • Verwendungsmöglichkeiten für Transistoren
    • Welche Verwendungsmöglichkeiten gibt es für Transistoren?
    • Zeichnen Sie einen Spannungsverdoppler.
    • Was ist ein Pegelwandler?
    • Warum werden heutzutage bevorzugt Feldeffekt-Transistoren und nicht Bipolartransistoren verwendet?

mit Antworten

Welche der folgenden Aussage(n) ist/sind mit Blick auf das Bild oben richtig?
Welche Aussage(n) zur Bipolartransistoren ist/sind korrekt?
Welche Aussage(n) zur MOSFETs ist/sind korrekt?
You Scored % - /

Bildreferenzen

Referenzen zu den genutzten Medien
Element Lizenz Link
Video: Stromkreiselemente - Dioden und Transistoren - Teil 4 CC-BY (Youtube) https://www.youtube.com/watch?v=KjyHta5p9WE
Abbildung 4: Funktion des npn-Bipolartransistors (c) Open Music Lab, mit Genehmigung der Weiterverwendung Quelle: Mail des Illustrators
Abbildung 5: Funktion des MOSFETs (c) Open Music Lab, mit Genehmigung der Weiterverwendung CrowdSupply
1) In der Praxis wird noch zwischen der Kleinsignal-Stromverstärkung $\beta = h_{fe}$ und Großsignal-Stromverstärkung $B = h_{FE}$ unterschieden. Beim Kleinsignalverhalten wird eine relativ kleine Änderung um einen festen Arbeitspunkt (z.B. um bestimmte Werte $I_C$ und $U_{CE}$) betrachtet. Beim Großsignalverhalten wird eine Änderung zwischen 0 und einem gegebenen Wert betrachtet. Bei nichtlinearen Kenngrößen können sich beide Größen unterscheiden. In diesem Kurs wird nur das Kleinsignalverhalten beschrieben. Das Großsignalverhalten und die Unterscheidung beider Betrachtungen wird in diesem Kurs nicht betrachtet.
2), 3) Bei den Feldeffekt-Transistoren bildet sich zusätzlich ein Kondensator zwischen Source und Drain aus, welcher insbesondere beim schnellen Schalten von Induktivitäten zu Überspannungen am MOSFET führen kann.